Collatzova domnienka - II. diel: Fraktálne štruktúry a všeobecné rovnice
Úvod
Tento článok bude o ďalších nápadoch ku Collatzovej domnienke (Collatz conjecture). Tento problém je tiež známy pod názvami 3n + 1 problém, Ulamov problém (podľa Stanisława Ulama), Kakutanov problém (podľa Šizua Kakutaniho), Thwaitov problém (podľa sira Bryana Thwaitesa), Hassov algoritmus (podľa Helmuta Hasseho) alebo tiež ako Syrakuský problém.
Tento článok priamo nadväzuje na prvý diel o Collatzovej domnienke.
Hľadanie všeobecnej rovnice
V úvodnom článku sme dospeli k tomu, že dokážeme nájsť všeobecné riešenie pre ľubovoľný fraktál. Tie najzákladnejšie sú znázornené na obrázku 1.
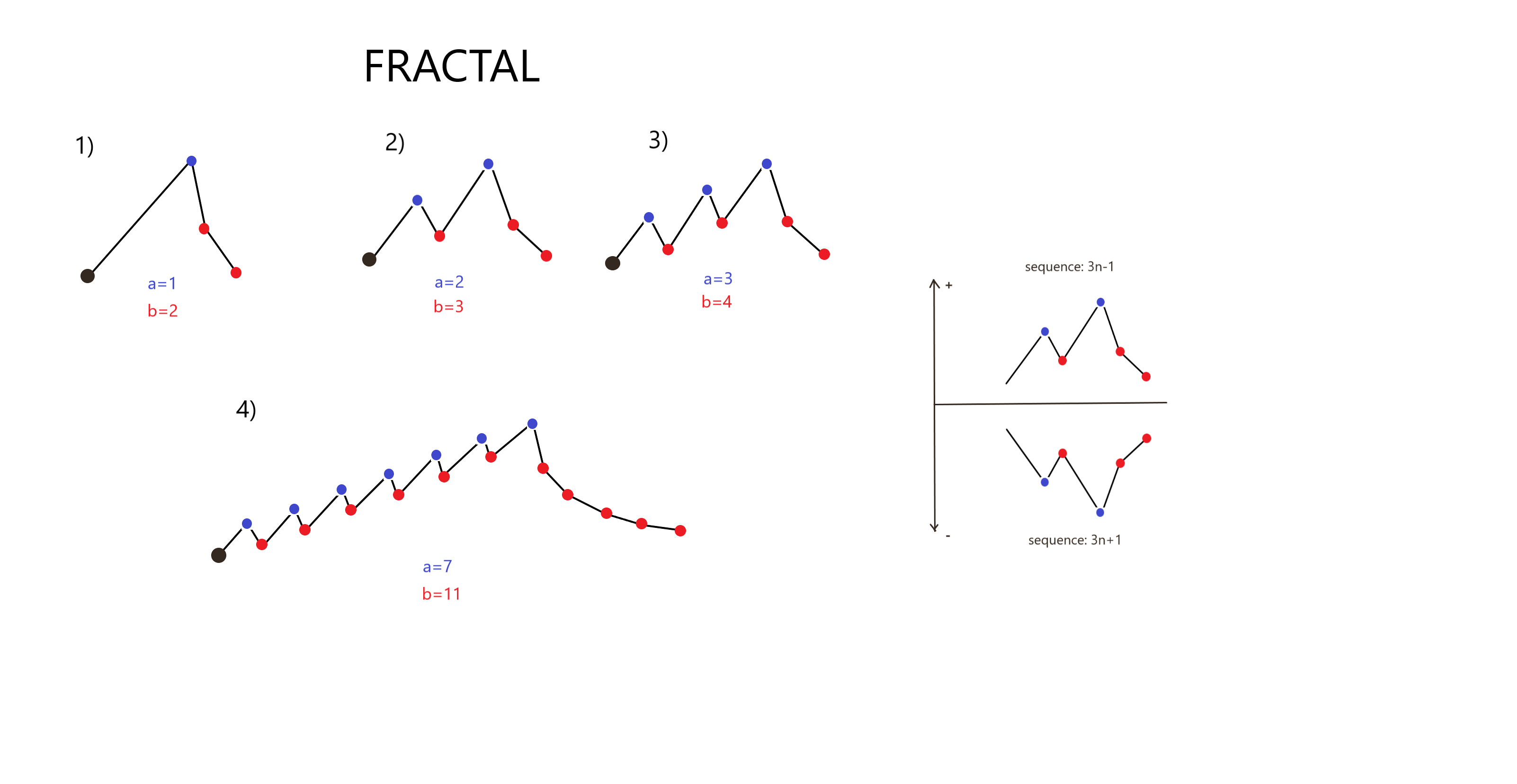
Obr. 1: Základné fraktály pre sekvenciu 3n-1
Sekvencia 3n-1 je užitočná aj v tom, že celočíselné, záporné riešenie rovníc jednotlivých fraktálov je zároveň riešením Collatzovej hypotézy 3n+1. To je schematicky znázornené na obrázku 1.
Odvodenie rovníc pre fraktály
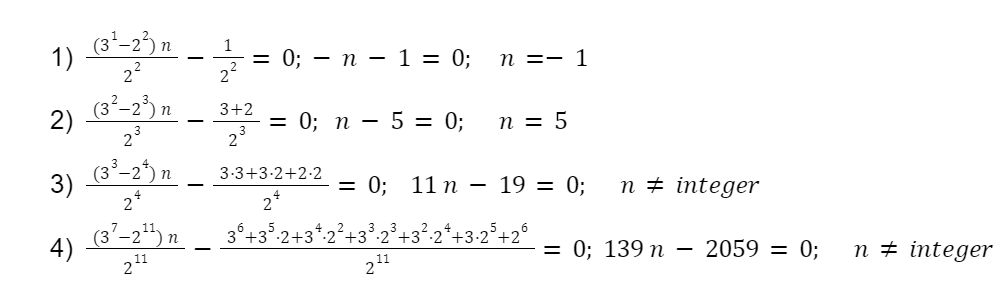
Všimnime si, že pre ľubovoľný n-fraktál takéhoto typu vznikne všeobecná rovnica:

Rovnice (1.8) až (1.11) dávajú jednoduché riešenie n-tého fraktálu v zmysle obr.1. To by sa dalo preveriť ľubovoľne ďaleko (s ohľadom na výpočtovú náročnosť). Možno rovnica (1.11) umožní vytvoriť dôkaz pre n-fraktál, pričom n smeruje k nekonečnu.
Bohužiaľ, ak urobíme miernu zmenu v type fraktálu, ako je znázornené na obrázku 2, zistíme, že rovnice pre túto zmenu sú síce podobné, ale nie identické.
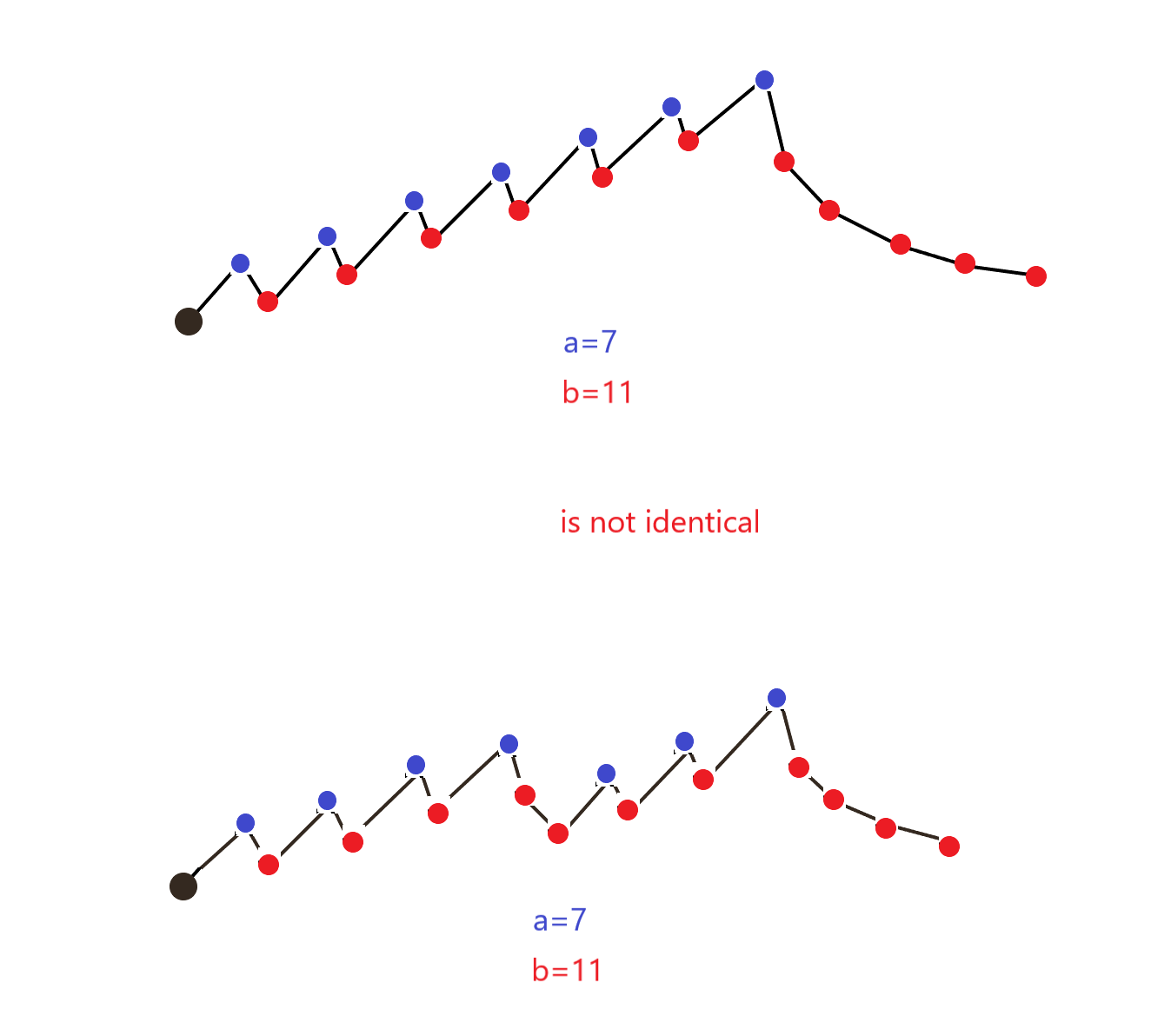
Obr. 2: Porovnanie fraktálov a ich rovnice
Výpočet pre dve varianty
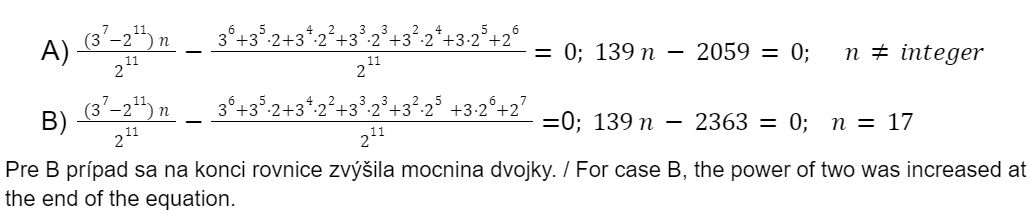
Tvrdenie (Statement)
To znamená, že rôzne variácie fraktálov vedú na kombinatorickú explóziu.
This means that different variations of fractals lead to a combinatorial explosion.
Rovnica (1.10) sa dá upraviť na jednoduchšiu rovnicu:
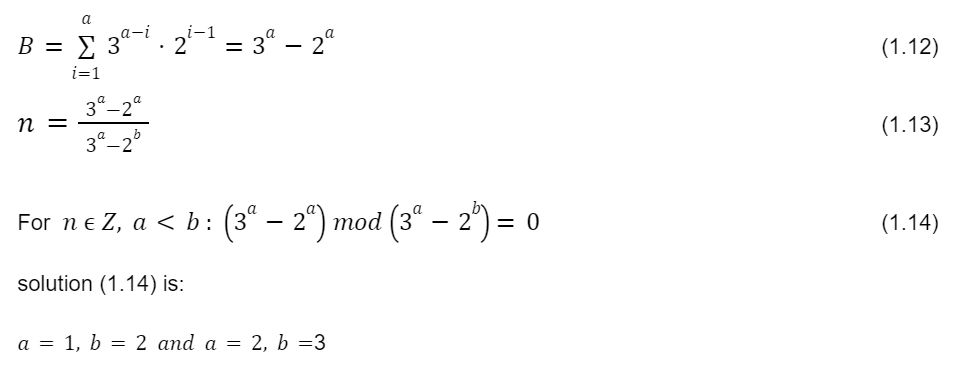
Riešenie môžete preveriť aj pomocou Wolfram Alpha:
Wolfram Alpha - riešenie rovnice
Intuitívne by sme povedali, že riešenie (1.14) je pre dva prípady skôr výnimka (s malými číslami) ako pravidlo. Začiatok a koniec na rovnakej úrovni dostaneme len pre tieto dva prípady (viď vyššie). Môžeme urobiť malú konštrukciu dôkazu.
Test závislosti
Na to, aby fraktál (obr. 2) mohol skončiť na rovnakej úrovni, existuje závislosť medzi "a" a "b". Táto závislosť je nasledovná:

Dostali sme rovnicu s jednou premennou. Pozrime sa na priebeh tejto rovnice.
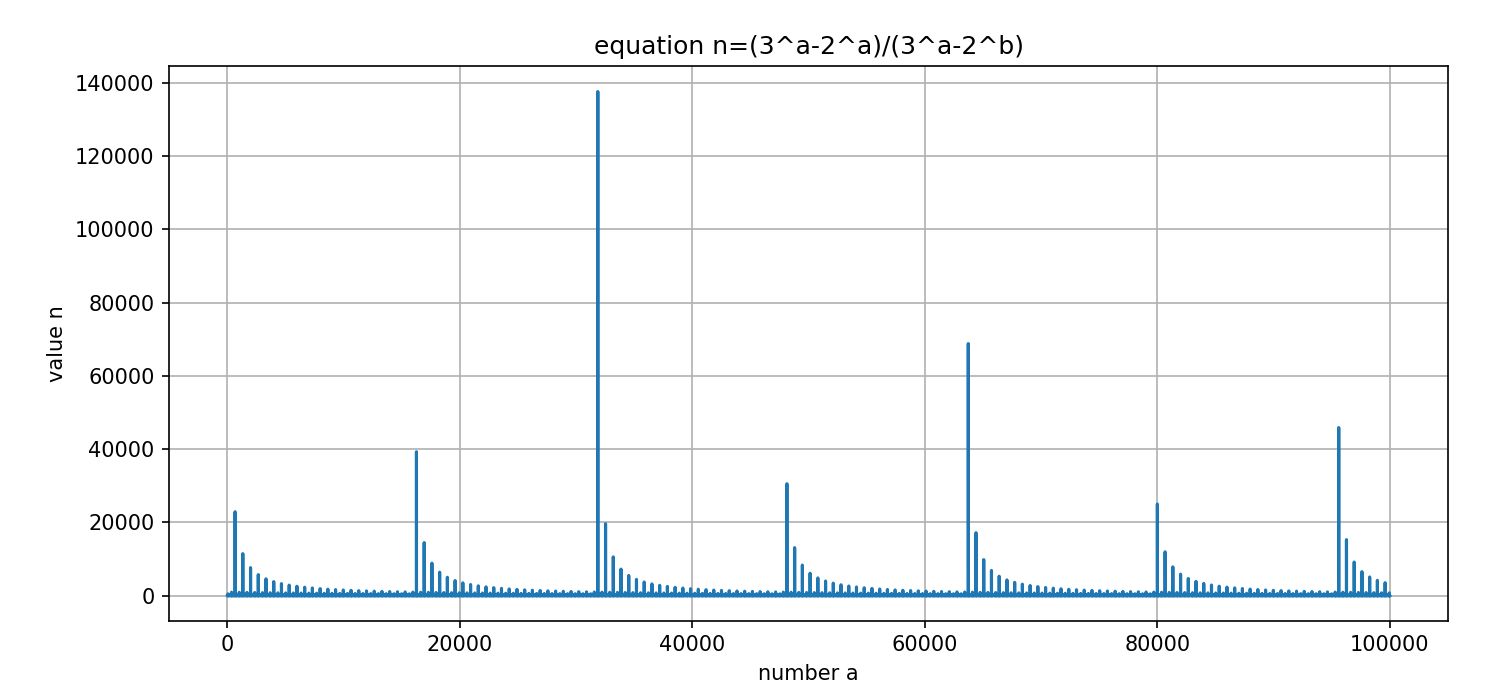
Obr. 3: Priebeh rovnice 1.16
V tomto intervale nebola nájdená celočíselná hodnota pre n (iná ako sú uvedené riešenia). Počítač preveril 2 až 100-tisícový fraktál. Priebeh funkcie je prekvapivý. Priebeh je fraktálny, pričom pre zaujímavosť sa zmeny opakujú v rovnakých vzdialenostiach (pre rast), aj u poklesu sú rovnaké vzdialenosti, napr. perióda 665, perióda 15601 atď.
Priebeh zvyškov po delení (modulo) je znázornený na obrázku 4. Pre a>20 sú zvyšky >1 000 000 a čoraz viac sa zvyšujú. Na celom skúmanom intervale neklesne zvyšok ani raz pod 1 milión.
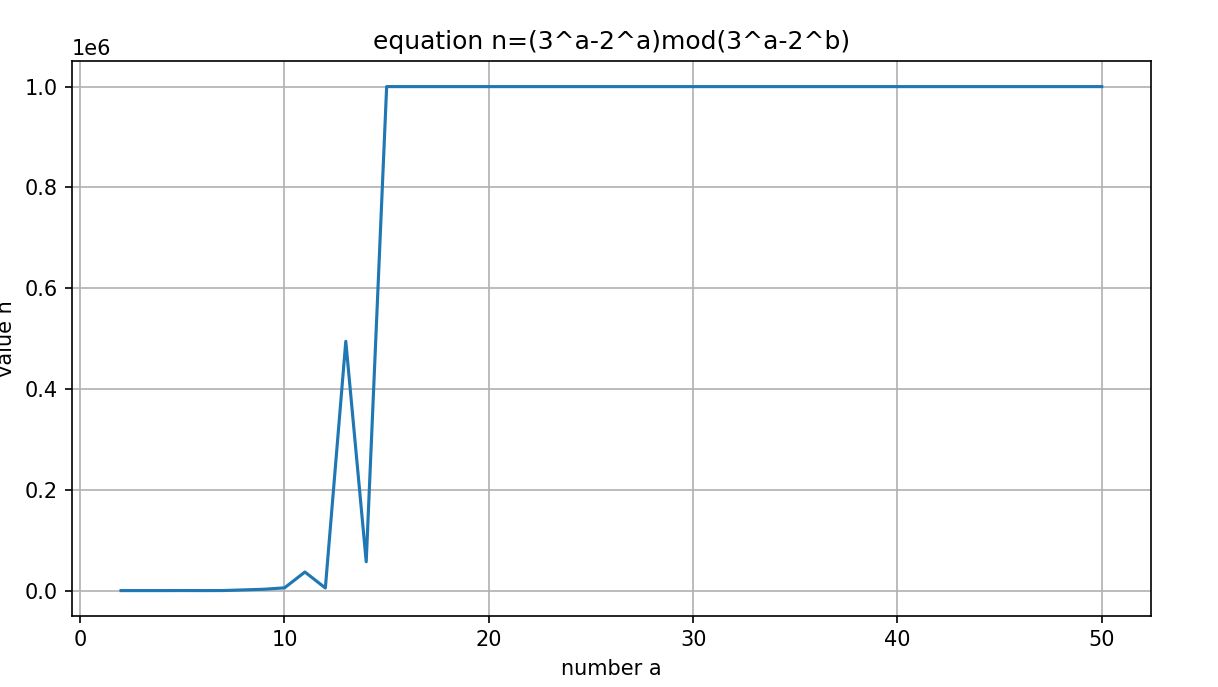
Obr. 4: Priebeh zvyškov je pre a>20 vždy väčší ako 1 milión. Skúmané na intervale 1-100 000.
Predpoklad je teda, že zvyšky už menšie nebudú až do nekonečna. To nie je prekvapivé.
Konštrukcia dôkazu


Záver
Na záver tohto článku malá rekapitulácia. Podarilo sa nájsť všeobecnú rovnicu pre fraktál z obr. 1, ktorý je n-rozmerný a ten najjednoduchší. Preveril sa fraktál pre n=1 až n=100 000 s programom v Pythone.
Bol vytvorený dôkaz, že okrem uvedených riešení už neexistuje iný fraktál, ktorý spĺňa rovnicu (1.17) a (1.18). Tento dôkaz možno poslúži aj pre hľadanie dôkazu všeobecného fraktálu s n vrcholmi (teda možnej opakujúcej sa sekvencie).