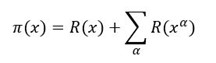
Riemannová hypotéza:

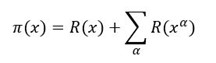
Pokiaľ Riemannová hypotéza platí, potom je možné priebeh prvočísiel v celkovom počte nahradiť uvedenou funkciou, viď. Obr.1.

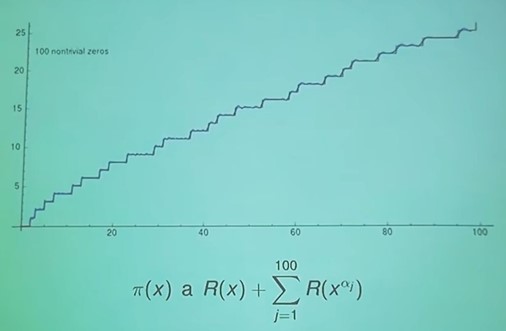
Obr.1 - Preložená Riemannova funkcia aproximuje presne π(x) v nekonečnom rade.

The Riemann Hypothesis Says 5040 is the Last

Existuje veľa ekvivalentných spôsobov ako Riemannovú hypotézu formulovať. Zameriam sa na tento výklad. (zdroj: výkladu).

Zoberme si ľubovoľné kladné, celé číslo N, napr. N=12. Teraz si zoberme všetkých deliteľov tohto čísla bezo zvyšku postupne a sčítajme výsledok:

V roku 1984 Gay Robin ukázal, že Riemannova hypotéza je ekvivalentná tvrdeniu, že pre každé číslo N>5040 platí:

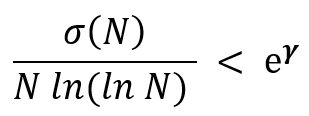
Pričom je Eulerova-Mascheroniho konštanta daná vzťahom:

Príklad:

Napr. číslo N=5040:

Priebeh jednotlivých čísiel >10 je na obr.2.

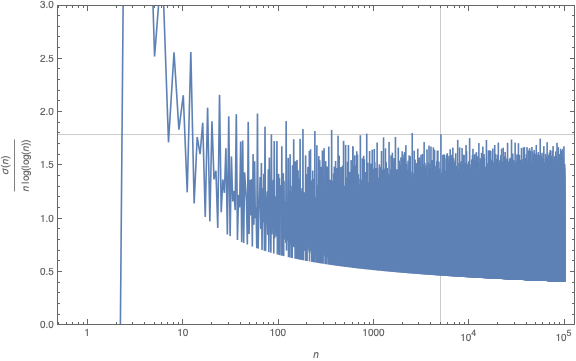
Obr. 2 Gay Robin index, zdroj: golem.ph.utexas.edu

Napr. niektoré blízke vrcholy sú:

(7560, 1.739917)

(10080, 1.755814)

(55440, 1.751247)

(110880, 1.734849)

(720720, 1.733065)

Výpočet sigma

Autor: Robopol

Pre využitie efektívneho algoritmu, pre výpočet tohto indexu potrebujeme vytvoriť vzťah sigma (N). Každé zložené číslo sa dá rozložiť na súčin prvočísiel. Tu sa jedná hlavne o prípady, kedy máme číslo N zadané v rozklade na prvočísla.

Najjednoduchší prípad je:

potom platí:

zložitejší prípad:

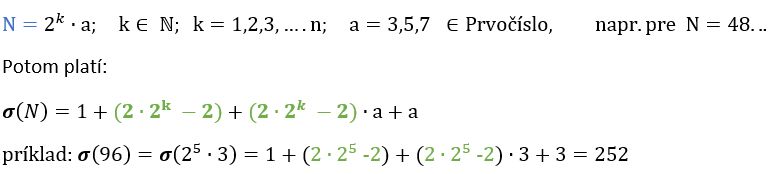
Tu si môžete všimnúť, že vzniká kombinačná metóda so vzorčekmi, ktorá je podstatne efektívnejšia ako rátať sigmu tak, že budeme deliť všetky čísla od 1 po N, pokiaľ máme číslo rozložené na súčin prvočísiel. Poďme na zložitejšie prípady.

V súčine sa môžu objaviť mocniny pre iné základy:

Postupne sa dostávame k univerzálnemu vzťahu pre výpočet sigma, ešte predtým urobíme jeden zložitejší príklad pre N=5040. Tu zistíme, že robíme kombinácie, každého člena s každým:

---

Načo boli tieto rozklady dobre? Okrem toho, že to poskytuje výhodu rýchlo zrátať nádejných kandidátov na potvrdenie/nepotvrdenie Riemannovej hypotézy, tieto rozklady v sebe ukrývajú oveľa viac ako sa na prvý pohľad zdá. Tu začína tá pekná časť matematiky.