Úvod do Riemannovej hypotézy

Introduction to the Riemann Hypothesis

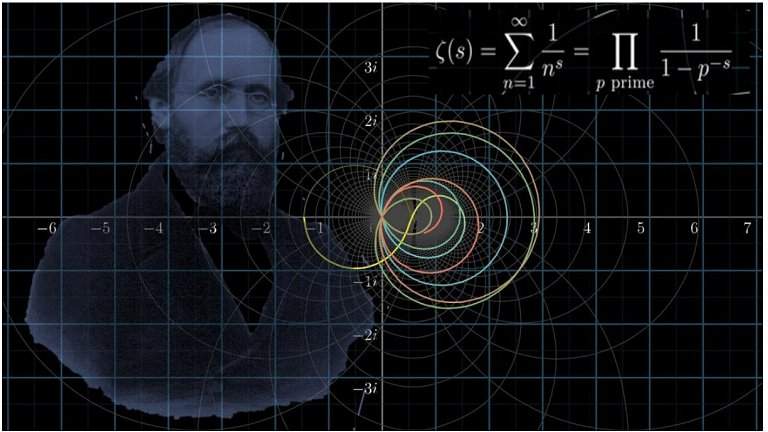
Riemannova hypotéza je jedným z najvýznamnejších nevyriešených problémov v matematike. Bola formulovaná nemeckým matematikom Bernhardom Riemannom v roku 1859 a týka sa distribúcie prvočísel. Hypotéza predpokladá, že všetky netriviálne nulové body Riemannovej zeta funkcie ležia na kritickej priamke s reálnou časťou 1/2.

The Riemann Hypothesis is one of the most significant unsolved problems in mathematics. It was formulated by the German mathematician Bernhard Riemann in 1859 and concerns the distribution of prime numbers. The hypothesis assumes that all non-trivial zeros of the Riemann zeta function lie on the critical line with real part 1/2.

Tento problém je natoľko významný, že bol zaradený medzi sedem Millenium Prize Problems Clayovho matematického inštitútu, s odmenou 1 milión dolárov za jeho vyriešenie.

This problem is so significant that it was included among the seven Millennium Prize Problems of the Clay Mathematics Institute, with a reward of 1 million dollars for its solution.

Ekvivalentné podmienky pre Riemannovu hypotézu

Equivalent Conditions for the Riemann Hypothesis

Počas rokov výskumu bolo objavených niekoľko ekvivalentných podmienok pre Riemannovu hypotézu. Tieto podmienky poskytujú alternatívne spôsoby, ako dokázať alebo vyvrátiť hypotézu. Medzi najznámejšie patria:

Over the years of research, several equivalent conditions for the Riemann Hypothesis have been discovered. These conditions provide alternative ways to prove or disprove the hypothesis. Among the most famous are:

• Robinova nerovnosť - Guy Robin dokázal, že Riemannova hypotéza je ekvivalentná s nerovnosťou σ(n) < e^γ · n · ln(ln(n)) pre všetky n > 5040, kde σ(n) je suma deliteľov čísla n a γ je Eulerova konštanta.
• Lagariasova nerovnosť - Jeffrey Lagarias formuloval ekvivalentnú podmienku, že σ(n) ≤ H_n + e^H_n · ln(H_n) pre všetky n > 1, kde H_n je n-té harmonické číslo.
• Ramanudžanova podmienka - Srinivasa Ramanujan navrhol ekvivalentnú podmienku týkajúcu sa veľkosti funkcie τ(n), ktorá počíta počet deliteľov čísla n.

• Robin's inequality - Guy Robin proved that the Riemann Hypothesis is equivalent to the inequality σ(n) < e^γ · n · ln(ln(n)) for all n > 5040, where σ(n) is the sum of divisors of n and γ is Euler's constant.
• Lagarias's inequality - Jeffrey Lagarias formulated an equivalent condition that σ(n) ≤ H_n + e^H_n · ln(H_n) for all n > 1, where H_n is the n-th harmonic number.
• Ramanujan's condition - Srinivasa Ramanujan proposed an equivalent condition concerning the size of the function τ(n), which counts the number of divisors of n.

Môj výskum sa zameriava na testovanie a dokazovanie týchto ekvivalentných podmienok pomocou počítačových algoritmov a matematickej analýzy.

My research focuses on testing and proving these equivalent conditions using computer algorithms and mathematical analysis.

Výskumné programy a nástroje

Research Programs and Tools

V rámci výskumu Riemannovej hypotézy som vyvinul niekoľko programov v jazyku Python, ktoré umožňujú testovať rôzne aspekty hypotézy a jej ekvivalentných podmienok:

As part of my research on the Riemann Hypothesis, I developed several programs in Python that allow testing various aspects of the hypothesis and its equivalent conditions:

Guy Robin index

Guy Robin Index

Program na výpočet Guy Robin indexu pre veľmi veľké čísla. Tento index je kľúčový pre testovanie Robinovej nerovnosti, ktorá je ekvivalentná s Riemannovou hypotézou.

A program for calculating the Guy Robin index for very large numbers. This index is key for testing Robin's inequality, which is equivalent to the Riemann Hypothesis.

Program umožňuje efektívne počítať hodnoty σ(n)/(n·ln(ln(n))) pre veľké hodnoty n a porovnávať ich s hodnotou e^γ, čo je približne 1.78107.

The program allows efficiently calculating values of σ(n)/(n·ln(ln(n))) for large values of n and comparing them with the value of e^γ, which is approximately 1.78107.

Viac informácií o programe Guy Robin index More information about the Guy Robin Index program

Program na testovanie platnosti Riemannovej hypotézy

Program for Testing the Validity of the Riemann Hypothesis

Komplexný program na testovanie platnosti Riemannovej hypotézy prostredníctvom jej ekvivalentných podmienok. Program umožňuje hľadať potenciálne protipríklady a overovať platnosť hypotézy pre veľké rozsahy čísel.

A comprehensive program for testing the validity of the Riemann Hypothesis through its equivalent conditions. The program allows searching for potential counterexamples and verifying the validity of the hypothesis for large ranges of numbers.

Viac informácií o programe na testovanie Riemannovej hypotézy More information about the program for testing the Riemann Hypothesis