Úvod
Tento diel je voľným pokračovaním na Prvočísla -5 diel, kde bol rozobratý geometrický aspekt malej Fermatovej vety. Tento diel bude zovšeobecnením a upresnením toho, ako by sa dali hľadať efektívne veľké prvočísla. Keďže metóda je postavená na malej Fermatovej vete, nie je 100% záruka, že nájdeme prvočíslo, no pravdepodobnosť určenia prvočísla je veľmi vysoká (99,99..%)
Fermatová veta nie je 100% nástroj na určenie
prvočísla. Tento problém sa rieši tak, že sa vyskúšajú aj iné základy pre a=2,3,4,....N. Testy ukázali, že pri aplikácii rovníc a k ním
prislúchajúcich originálnych zvyškov MUSIA platiť pre naozaj veľký rozsah
prvočísiel. Presne sa to dá dohľadať v literatúre.
Napr. pre tieto neplatí:

Tieto nedostatky malej Fermatovej vety sa riešia napr. takto:
zdroj: thales.doa.fmph.uniba.sk/sleziak/papers/aks.pdf
Dnes zhrnieme, čo testy ďalej ukazujú:
Pozitívna správa je, že nám vypadli rovnice, ktoré v algoritme nedávajú test prvočíselnosti. To znamená, že potrebné sú len tieto vzťahy:

Poznámka:
Ak preveríme rovnice pre y- smer, nie je potrebné úž preverovať rovnice pre x - smer, pretože sú vzájomne závislé. Toto tvrdenie platí aj naopak. Ak preverujeme rovnice pre x - smer, nie je potrebné preverovať pre y- smer. Vysvetlenie, prečo je tomu, viď nižšie.
Delenie intervalu 2ˆp
V predchádzajúcom diely o prvočíslach bolo konštatované, že orezávanie pôvodnej plochy cez periódu čísiel, teda zmenšovanie plochy 2ˆp číslom 10 ˆr*p, pre r=1,2,3.... nie je účinné, v zmysle zníženia výpočtovej náročnosti (veľké prvočísla – viď. diel prvočísla 5 diel).
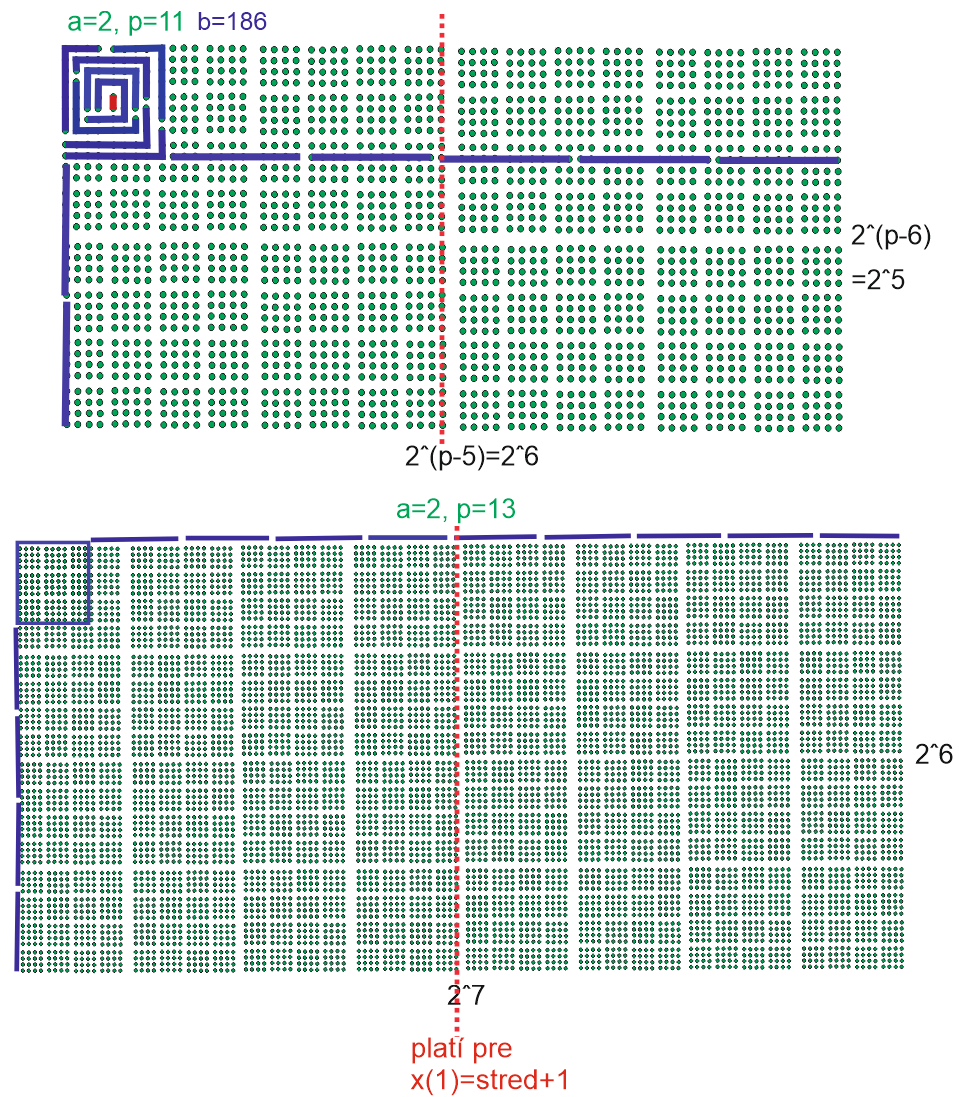
Obr.1 Príklad delenia os – x, pre p=11, p=13, zdroj: vlastný obrázok.
Pri delení plochy v zmysle. Obr.1 nám prvočísla končia pre os x zvyšok x(1)-> stred+1, teda v príklade to je: 2 ˆ(int(p/2)+1)/2+1=2 ˆint(p/2)+1. Tam končia prvočísla (v zmysle celočíselného násobku). Zistíme však, že všeobecne platí pre všetky prvočísla os x, v zmysle obr.2.
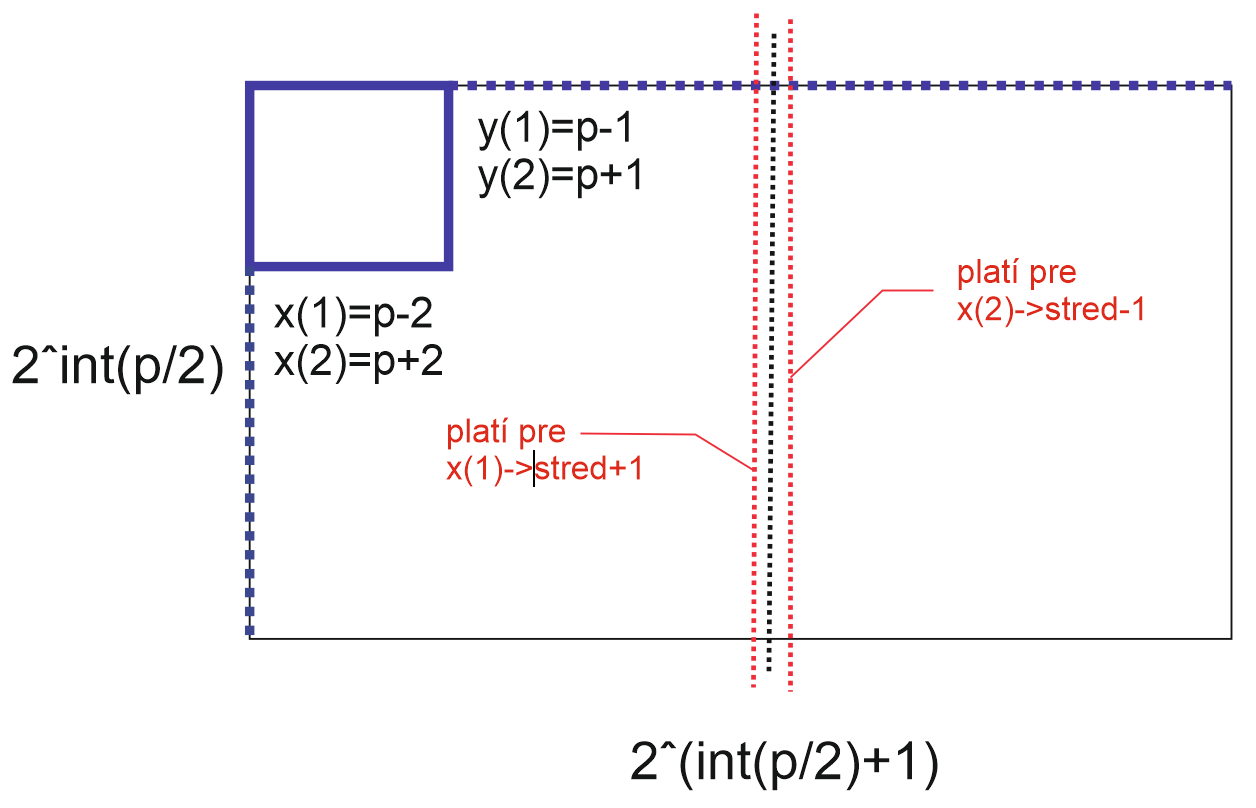
Obr. 2 Predelenie os x, pre p=prvočíslo, zdroj: vlastný obrázok.
Všeobecne teda platí pre zvyšok x(1), že prvočísla končia -> stred+1, pre zvyšok x(2) končia -> stred -1.
Poďme túto novú vlastnosť použiť nasledovne:
Ak teda všetky prvočísla po predelení končia v polovici intervalu os : x +-1, potom teda musí platiť vzťah:
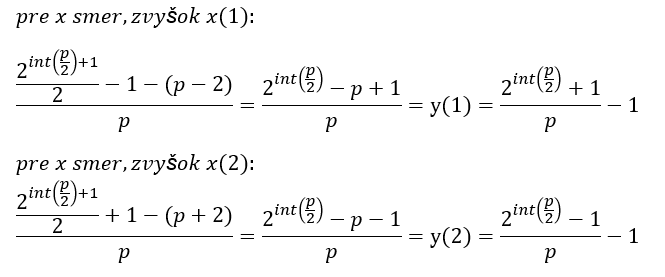
Dosadením tejto novej vlastnosti do vzťahov dostaneme identické vzťahy pre y(1), y(2), viď. vzťahy vyššie. Z toho plynie záver ten, že postačuje nám preveriť iba dve rovnice, viď. algoritmus výpočtu.
Z tejto vlastnosti obr.2 sa dajú vytvoriť jednoduchšie vzťahy (ako doposiaľ):

Mohli
by skúsiť predeliť na polovicu y-novú hodnotu 2 ˆint(p/2) a pozrieť
sa, kde budú končiť prvočísla (znížime výpočtovú náročnosť o jeden rad),
nájdeme tento vzťah:
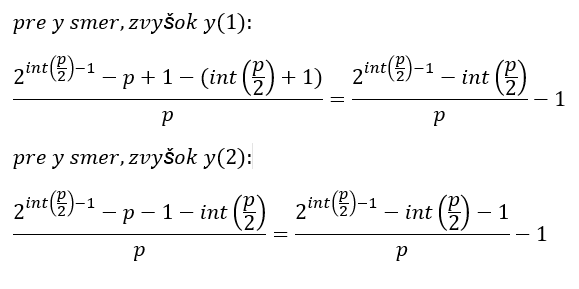
Čo, keby sme našli algoritmus, ktorý bude znižovať rád mocniny 2ˆint(p/2) o ľubovoľne veľkú hodnotu?
No zdá sa, že to také jednoduché nebude. Zatiaľ som našiel zhodu pre predelenie plochy na ½ a následne na ¼. Vzťahy sú vyššie. No takto jednoducho sa nebude dať pokračovať, pretože prvočísla nebudú v rovnakých pozíciách, pre ľubovoľné pridelenia intervalu (plochy).
Náročnosť výpočtu by sme mohli troška znížiť ešte tým, že pred samotným delením čitateľa menovateľom p, odčítame ešte hodnotu 2 ˆk*p. Z toho dostaneme vzťahy:
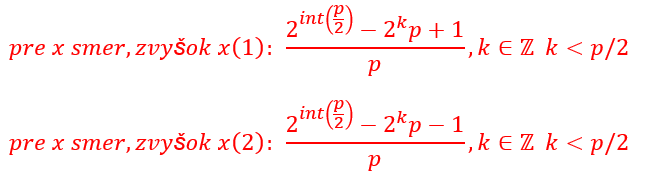
Upravený vzťah:
1 krok: preveriť 1rovnicu v 2 celkoch:
//dosadiť za p: preverované číslo
wolfram
https://www.wolframalpha.com/input/?i=%282%CB%86int%28p%2F2%29%2B1%29mod+p%3D
https://www.wolframalpha.com/input/?i=%282%CB%86int%28p%2F2%29-1%29modp%3D
ak výsledok je rozdielny od nuly, potom skúmané číslo nie je prvočíslo (veľká
pravdepodobnosť).
2.krok" ak vyšlo v jednej z rovníc :0, potom testované číslo je prvočíslo (veľká
pravdepodobnosť
).
Príklad:
P=1381
https://www.wolframalpha.com/input/?i=%282%CB%86int%281381%2F2%29%2B1%29mod1381%3D
mod 0, testované číslo je prvočíslo.
Záver
Takže zatiaľ som sa dostal k tejto formule, ktorá by mohla byť výpočtovo menej náročná, ako malá Fermatová veta, možno aj s použitím modulárnej aritmetiky (viď. príklady):


