Úvod
Tento diel je
pokračovaním predchádzajúceho článku (viď. odkaz), ktorý je venovaný
platnosti/neplatnosti Riemannovej hypotézy. V tomto diele sa pokúsime
pokročiť a pospájať doposiaľ zverejnené súvislosti. Uvedené vzťahy boli naprogramované a ich priebeh je zobrazený v jednotlivých grafoch.
Program
na adrese:
http://www.poling.sk/Riemann/publish.htm
Nájdete inštalačný program pre testovanie Riemannovej hypotézy v zmysle tohto článku.
Stiahnite
si inštalačný súbor, nainštalujte do PC (súbor
setup.exe), nainštaluje sa Vám ikona v ponuke štart, súbor je
bezpečný, povoľte nainštalovať súbor cez antivírovú ochranu.
Program má obmedzenie veľkosti čísiel a rýchlosti použitého algoritmu. Samozrejme tieto obmedzenia sa dajú zmeniť aj na väčšie čísla s využitím rozkladu na prvočísla a následne výpočtu sigmy cez všetky kombinácie (viď. prvý diel).
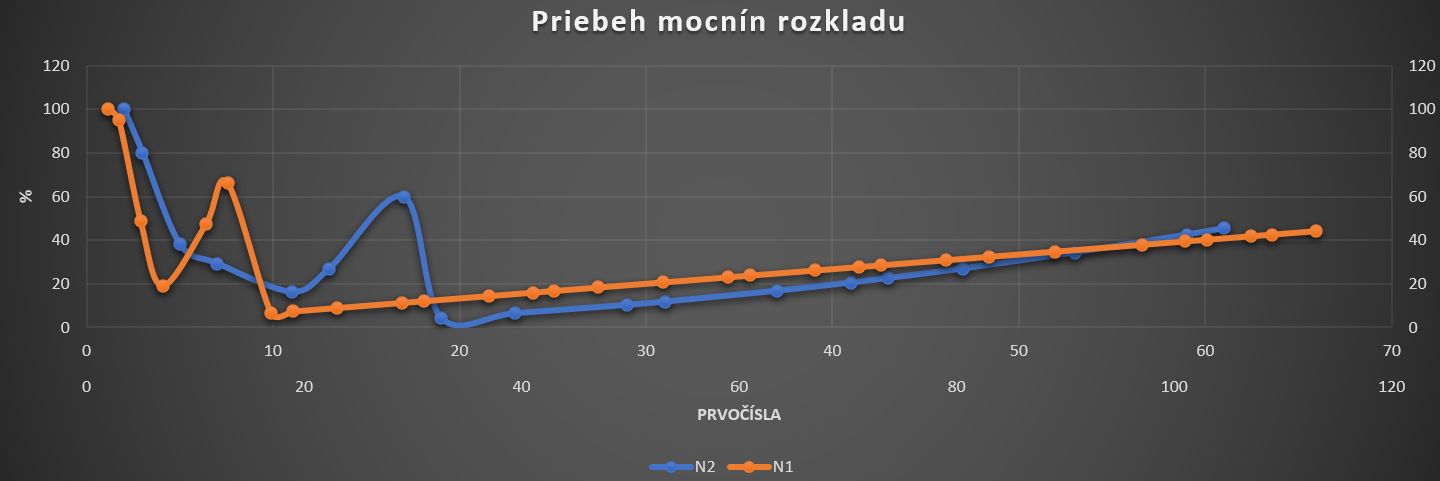
Nereálny počet deliteľov
Skúsme vypočítať priebeh, resp. limitu prípadu, kedy každé číslo má počet deliteľov od 1 po N. Celkom teda je počet deliteľov čísla N = N.
Z toho odvodíme súčet radu:
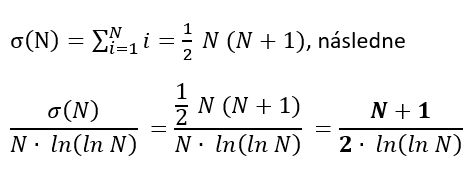
Priebeh takejto funkcie je na obr. 6
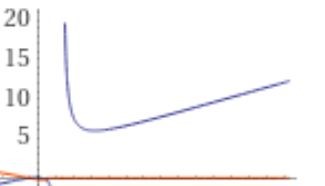
Obr. 6 Priebeh funkcie (N+1)/(2 ln(ln N)), zdroj: vlastný obrázok
Limita tejto funkcie je:
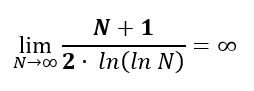
Pre nereálny prípad, že číslo N má všetkých deliteľov, teda počet deliteľov čísla N je znova N máme stúpajúcu funkciu indexu a limita je nekonečno.
Keďže nemáme analytické funkcie sigmy pre rôzne prvočíselné rozvoje musíme sa pozrieť na priebeh empiricky. Vytvoríme jednoduchý program na výpočet sigmy, sigma/N a Gay Robin indexu. Vytvoríme to pre tri varianty:
- Pattern prvočísiel v súčine za sebou
- Pattern prirodzených čísiel v súčine za sebou
- Ideálny pattern
Pattern prvočísiel v súčine za sebou
Ide o pattern, ktorý nám ukáže ako sa to správa pri dlhom rozvoji súčinu prvočísiel, bez mocnín prvočísiel.
To je prípad:

Tabuľka
zistených hodnôt:
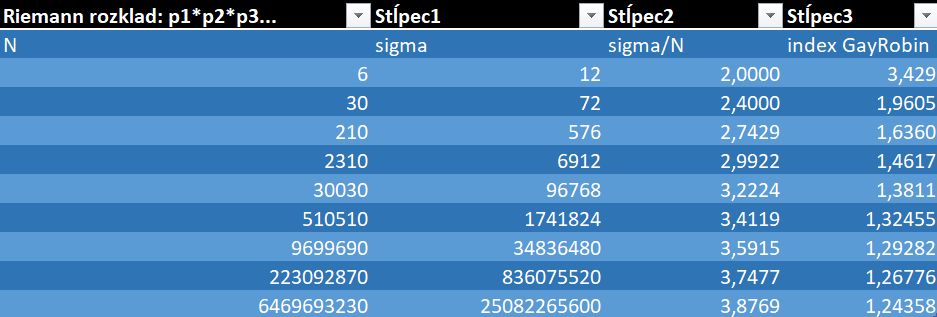
Jednotlivé priebehy:
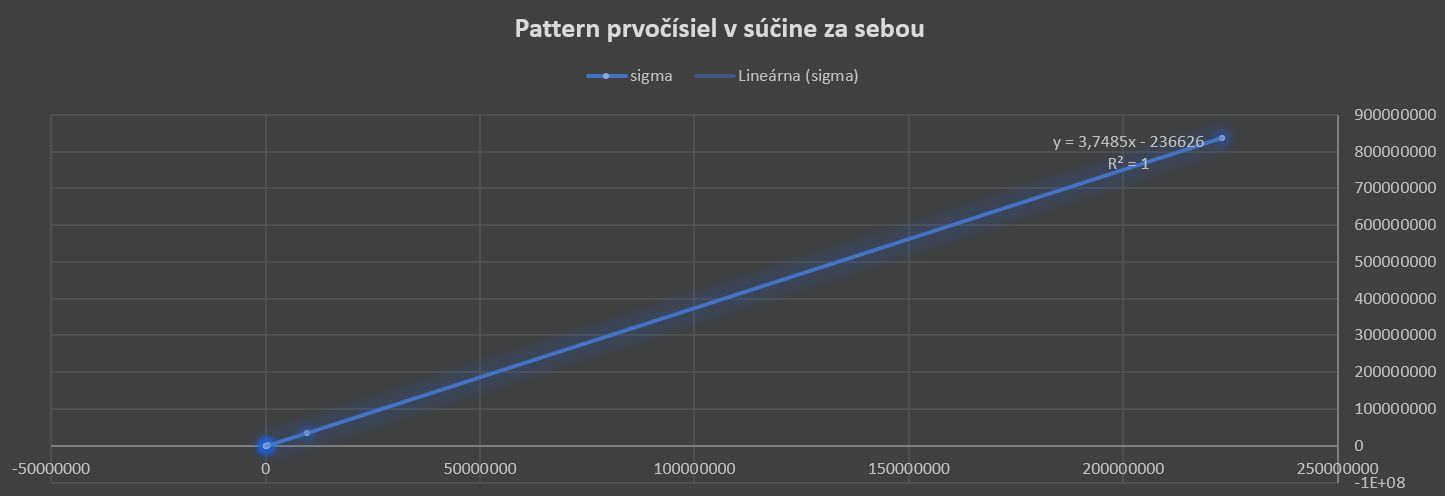
Obr.7 Priebeh sigma z tabulky, zdroj: vlastný obrázok.
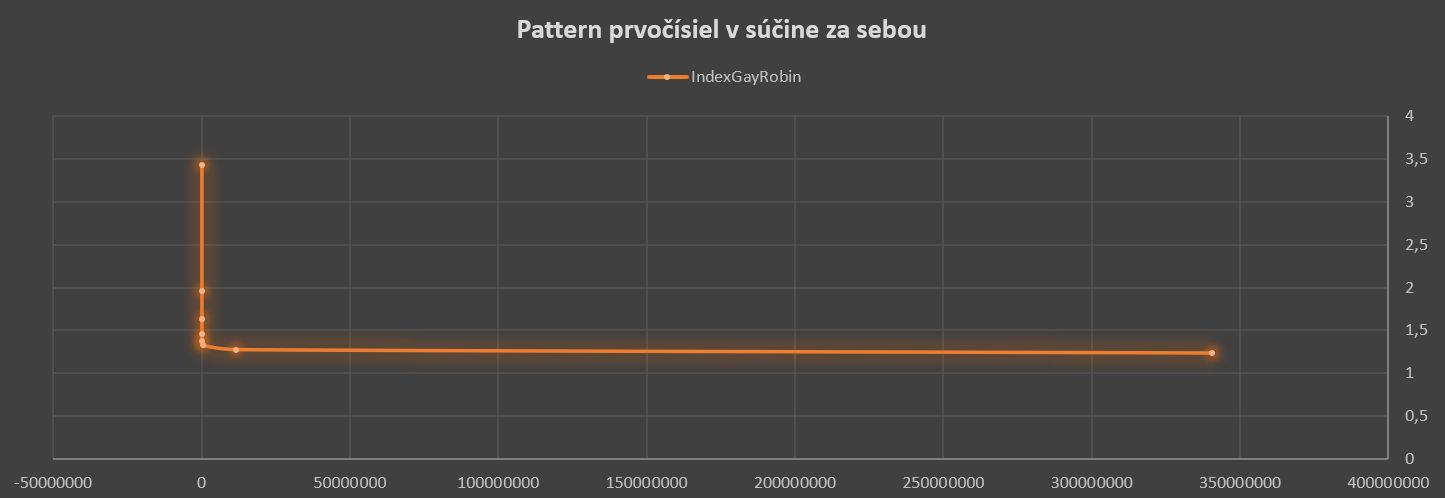
Obr. 8 GayRobin index z tabuľky, zdroj: vlastný obrázok.
Vyhodnotenie:
Pre tento pattern je vidieť, že Gay Robin index klesá (skoro v pravidelnej hodnote). Na grafe, pri sigme sa objavila korelácia hodnôt R=1 (Excel vyhodnotil), funkcia je uvedená na obrázku. Korelácia nie je presne rovná 1, no je to aproximácia (do hodnoty 223092870). Pre zaujímavosť limita Gay Robin indexu v takejto aproximácií je:
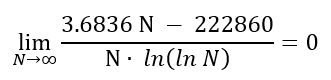
Zatiaľ je to empirický dôkaz na pár hodnotách (boli preverené aj väčšie), no v skutočnosti sa to principiálne nemôže nijak zmeniť, pretože tento pattern sa smerom k nekonečnu nemení.
Všimnime si z tabuľky nárast indexu =sigma/N. Celkom pravidelne narastá o nejakú delta hodnotu. Pokúsme sa nájsť aproximačný vzťah.
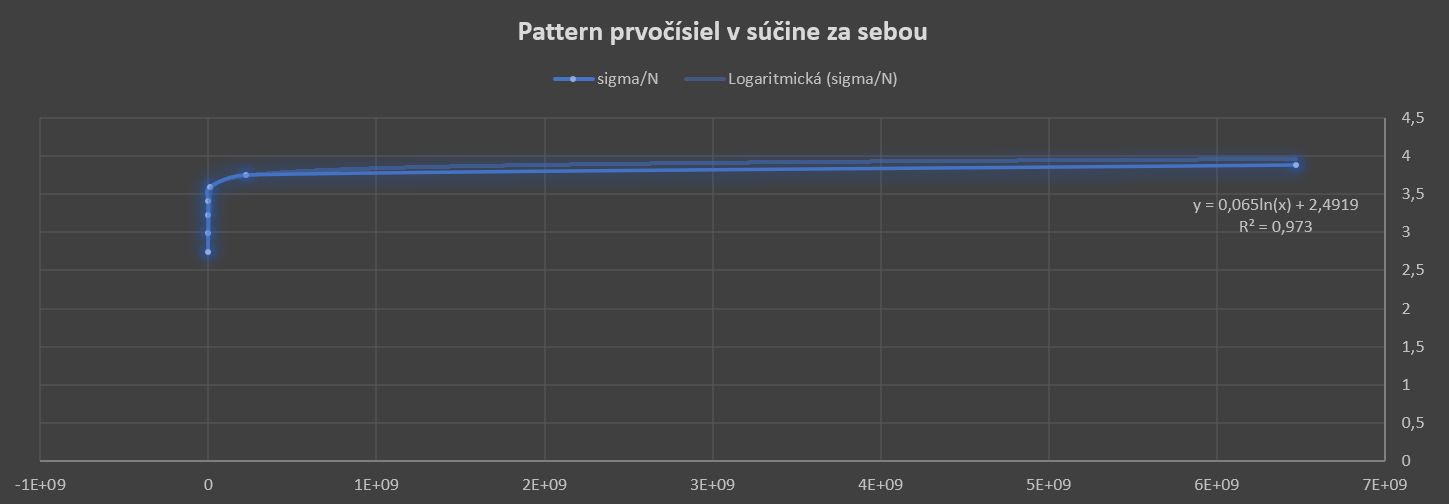
Obr.11 sigma/N z tabuľky, zdroj: vlastný obrázok
Na aproximácie je excel dobrý, ale iba na určitý úsek. Rovnako ako pre graf sigmy, táto aproximácia bude dobrá do hodnoty z tabuľky. Lepšie je však extrapolovať z prírastkov nejaký všeobecnejší/stabilnejší vzťah. Čitateľ si môže vytvoriť vlastnú koreláciu vzťahov. Rovnica y=0.065 ln(x)+2.4919 vyzerá ako horné ohraničenie skutočnej funkcie. To je dané tým, že smerom k nekonečnu sú prvočísla viac od seba vzdialené a tak klesá číslo (0.65) pred funkciou ln(x). Ak by sme dali kratší úsek napr. od čísla 210 po 223092870, tak bude aproximačná rovnica 0.0716 ln(x)+2,427. Pre číslo 6469693230 by bola hodnota sigma/n=0.0716*ln(6469693230)+2.427=4.044.
Pre rovnicu sigma/n= 0.065 ln( 6469693230 )+2.4919=3.96. To znamená, že ako zväčšujeme úsek aproximácie k vyšším číslam aproximačná funkcia klesá a teda to môžeme považovať za horné ohraničenie.
Dobre urobme limitu tejto funkcie dostaneme:
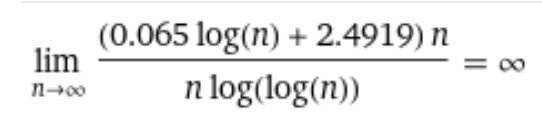
Horné ohraničenie teda konverguje k nekonečnu, teda sme zvolili veľmi prudký rast sigma/n. Toto ohraničenie nám teda nepomohlo. Zrejme je potrebné nájsť oveľa presnejší aproximačný vzťah horného ohraničenia odvíjajúc sa od :
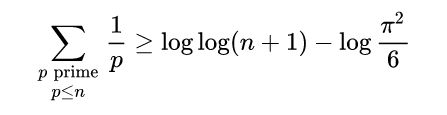
https://en.wikipedia.org/wiki/Divergence_of_the_sum_of_the_reciprocals_of_the_primes
Pattern prirodzených čísiel v súčine za sebou
Tento vzor je charakteristický mocninami prvočísiel, ktoré postupne klesajú, veľmi je podobný ideálnemu vzoru (pre maximalizáciu) sigmy.
Všeobecne to môžeme zapísať takto:

Tabuľka zistených hodnôt:
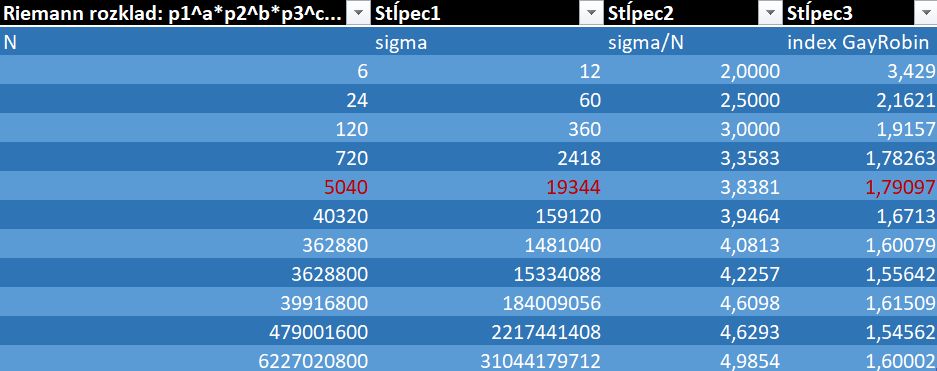
Jednotlivé priebehy:
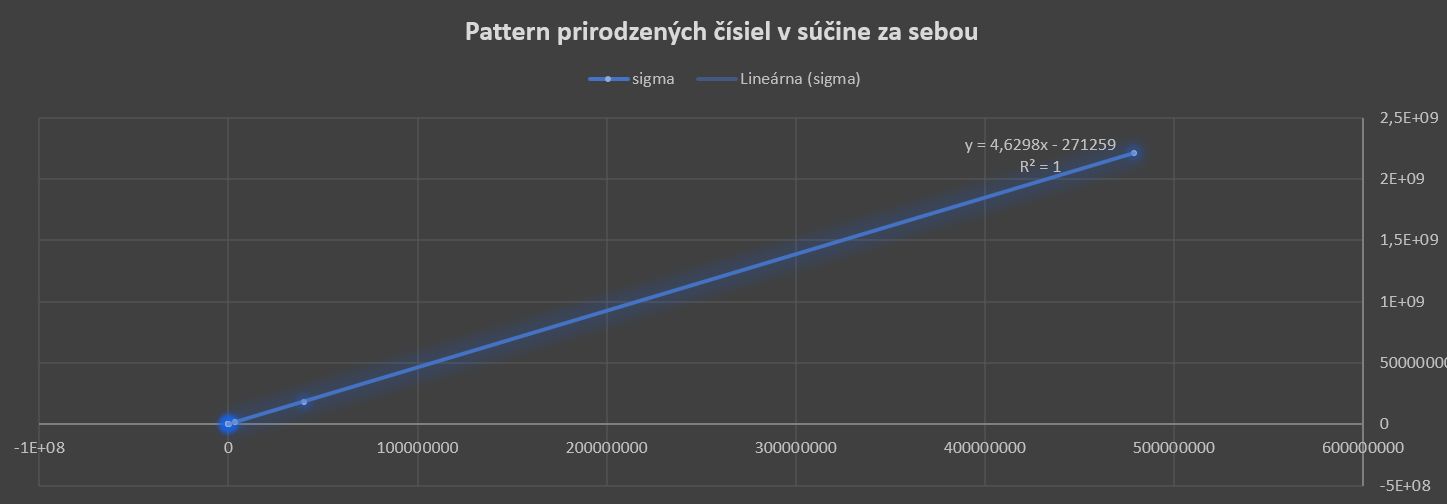
Obr.9 Priebeh sigma z tabulky, zdroj: vlastný obrázok.
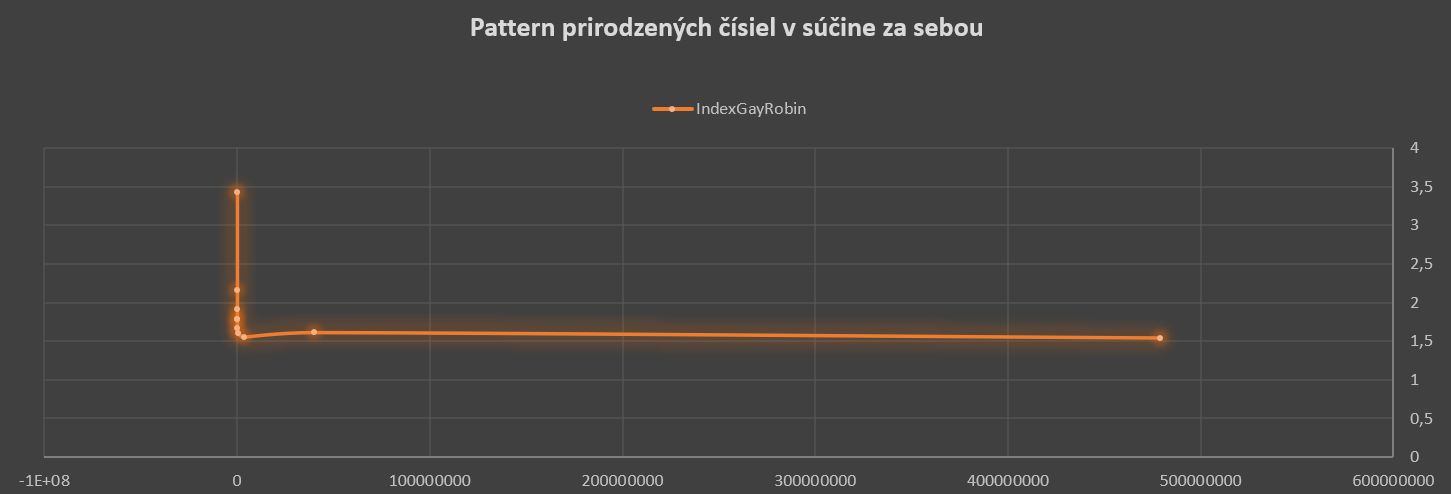
Vyhodnotenie:
Tento
vzor vychádza lepšie ako predchádzajúci, viď. tabuľka. Do tohto vzoru zapadlo
aj číslo 5040. Pri priebehu Gay Robin indexu dochádza k miernej oscilácii
hodnôt, kde neplatí, že nasledujúci index je vždy menší. To je dané tým, že
tento pattern za určitých okolnosti (ako je prípad 5040) sa priblíži k ideálnemu
patternu (taký, čo maximalizuje sigmu).
Najvyššie hodnoty tohto paternu získame pre hodnoty, viď. tabuľka

Tieto hodnoty získame tak, že pri rozvoji na N=2*3*4*5...posledné číslo (n) musí byť prvočíslo. Z tejto podmienky potom dostaneme rozvoj, ktorý postupne klesá. Na hrubo ho môžeme aproximovať funkciou (horné ohraničenie) viď. obr.12
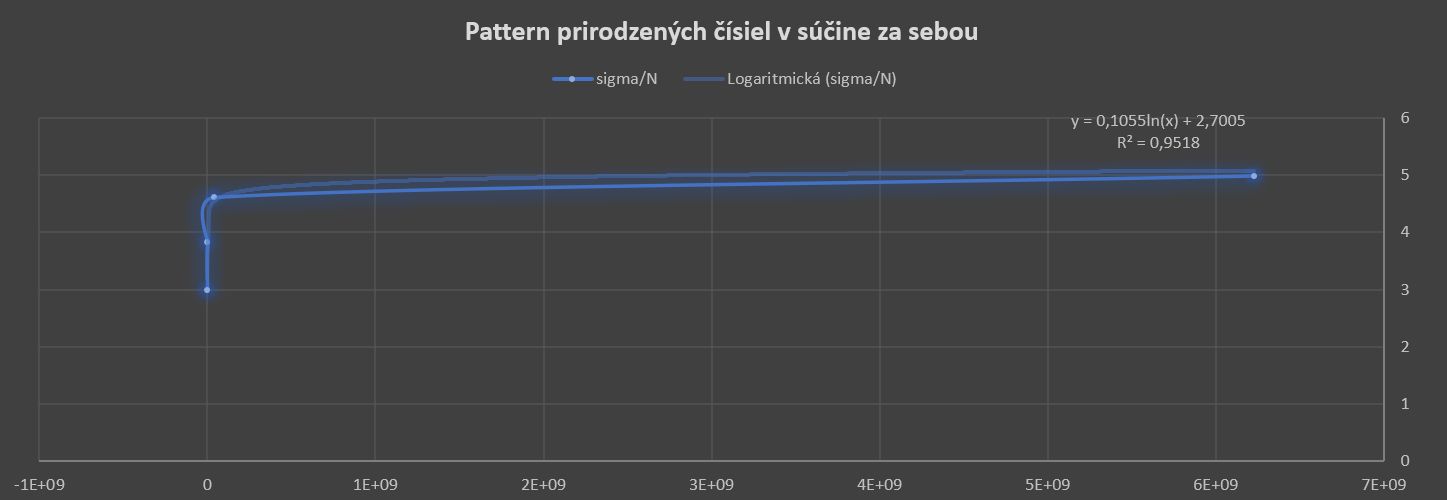
Obr.12 sigma/N z tabuľky, zdroj: vlastný obrázok
Presnejšie by sme získali horné ohraničenie pokiaľ by sme vypočítali ďalšie hodnoty z tabuľky. V našom prípade to je funkcia:
y=0,1055ln(x)+2,7005
limita tejto funkcie je:
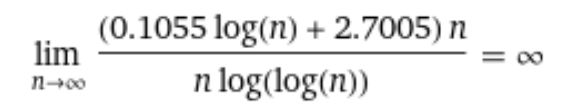
Horné ohraničenie teda konverguje k nekonečnu, teda sme zvolili veľmi prudký rast sigma/n. Toto ohraničenie nám teda nepomohlo.
Zrejme je potrebné nájsť oveľa presnejší aproximačný vzťah horného ohraničenia odvíjajúci sa od harmonickej rady:
https://en.wikipedia.org/wiki/Harmonic_series_(mathematics)
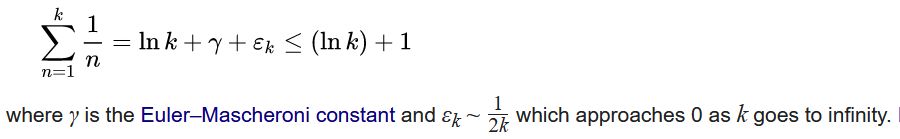
Ideálny pattern
Z týchto
dvoch vzorov (viď. vyššie) sa dá vyskladať ideálny pattern. Ideálny pattern je teda určitou
kombináciou % podielom prvého a druhého patternu. Empiricky však tieto dva
vzory ukazujú klesajúcu tendenciu smerom k nekonečnu. Klesajúci faktor je pozvoľný
no badateľný a smerom k nekonečnu spomaľuje.
V predchádzajúcom diely boli zobrazené (obr.5) dva ideálne vzory. Tento vzor vznikne najvýhodnejšou kombináciou predchádzajúcich dvoch vzorov. Pozostáva teda z vzoru (obr. 9,10) a vzoru – chvost (obr.7,8).
Pre tento pattern neexistuje jednoduchý predpis, preto
je znova potrebné použiť programovanie a preveriť to empiricky. Očakávame,
že rovnako ako predchádzajúce dva patterny by z princípu mal klesať (Gay
Robin index).
Vychádzajme z čísla 5040 a jeho rozvoja:

Na hrubo sa však dá konštatovať, že:
ideálny patern tak vznika pridaním dvoch koncových čísiel (chvost rozvoja) na zvýšenie jednej mocniny pre základ 2,3..atď. (viď. ideal pattern v programe na výpise čísiel). To platí pre čísla do 1*10 exp 12, pre čoraz väčšie čísla bude zrejme chvost (z prvočísiel) narastať viac na zvýšenie jednej mocniny, viď obr.6 z predchádzajúceho dielu.
Pre preverenie poklesu indexu pre ideálny pattern je však nutné preveriť oveľa väčšie čísla, aby sa dal urobiť vierohodný záver, čo vyžaduje preveriť správanie sa patternu, pre čísla do 1*10 exp 10000, resp.1*10 exp 100000. To vyžaduje výkonný počítač pre rátanie všetkých kombinácii rozkladu čísla na prvočísla (výpočet sigma), algoritmus pre rátanie veľkých čísiel (sigma, logoaritmus, atď.).
Záver
Na záver by zrejme bolo možné pre ideálny pattern vyčísliť mieru nárastu sigmy ( maximalizáciu), určiť jej horné ohraničenie (funkciu) z toho, že ideálny pattern je kombináciou uvedených dvoch vzorov, kde je potrebné detailne pochopiť, prečo práve určitá kombinácia (uvedených dvoch patternov) maximalizuje sigmu. To je dané tým, že pre pattern prirodzených čísiel v súčine za sebou dôjde k javu, kde sa generuje určite množstvo duplicít, teda príklad:
p=2*3*4*5*6
tak napríklad číslo 6 je deliteľom aj pre číslo
2*3*4*5, ale aj pre 4*5*6.
Teda pre výpočet sigmy môžeme prirátať číslo 6 len jedenkrát a duplicita, už nie je zahrnutá. Tento fakt teda ukazuje, prečo ideálny pattern je tak špecifický zostavený. No a existuje predpoklad, že táto miera duplicít nám môže ukázať súvislosť s menovateľom ln(lnN). V prípade zistenia teoretickej funkcie, pre maximálny možný nárast sigmy (ideálny pattern), by bolo už priamo dôkazom platnosti Riemannovej hypotézy.