Úvod

Tento diel bude venovaný niektorým aspektom prvočísiel v súvislosti s Riemanovou hypotézou. V predchádzajúcom diely https://robopol.sk/blog/prvocisla-a-pytagorejska-trojica-1-diel

boli stručne naznačené súvislosti s odkazom na Riemannovú hypotézu ( v stručnom videu od M. Rokytu, cz jazyk).

Tento matematický problém je zaujímavý, pretože ZETA funkcia nejakým spôsobom prepája záhadné prvočísla. Existuje na internete množstvo zdrojov k tejto téme. Práve preto, že sa jedná o dlho nevyriešený problém, napísal som pokračovanie na úvodný diel k tejto téme.

Pre pochopenie je potrebné sa zoznámiť s tou hypotézou, aj aparátom, ktorý sa v nej používa. V médiách prebehli informácie, že sa „podarilo“ nájsť dôkaz platnosti Riemanovej hypotézy od Michael Atiyaha. Ako je už zvykom snažím sa, aby každý článok priniesol niečo nové, zaujímavé.  Nekopírujem len cudzie myšlienky, ako to robí väčšina. Nevysvetľujem len to, čo už vieme.

Základné vlastnosti prvočísiel

Na základnej škole sme sa naučili, že prvočíslo má takú vlastnosť, že je deliteľné iba jednotkou a samým sebou. Základné prvočísla:

2           3           5           7           11         13         17         19         23         29

31         37         41         43         47         53         59         61         67         71 ....

To, čo nás pri prvočíslach najviac zaujíma je to, ako sú rozložené na číselnej osi.

Všimnime si , že platia tieto tvrdenia:

1.  Okrem 2 platí, že každé prvočíslo je nepárne číslo.

2. Platí, že žiadne prvočíslo, okrem prvočísla 5 nekončí päťkou. To má svoj dôvod taký, že akékoľvek veľké číslo napr. 150245785 je určite deliteľné päťkou.

3. Môžeme vytvoriť základný predpis v tvare j=(6k+-1), pričom k=1....n, j – možné prvočíslo. Predpis nám vlastne vytvára zoznam nepárnych čísiel.

4. Na to, aby sme zistili, či sa jedná o prvočíslo musíme použiť faktorizáciu. Základná metóda sa volá Eratostenovo sito.

5. Každé zložené číslo sa dá rozložiť na súčin prvočísiel.

Z uvedených tvrdení nutne plynie, že prvočísla nie sú na číselnej osi rozhádzané úplne chaoticky. Je v tom akýsi vnútorný poriadok súvisiaci so základnými vlastnosťami prvočísiel.

Väčšie prvočísla sa odvíjajú od menších prvočísiel, teda poloha prvočísiel na číselnej osi tesne súvisí s rozložením predchádzajúcich (menších) prvočísiel. Teda sa jedná o akýsi vnútorný vzťah medzi prvočíslami.

Gaussova funkcia

Prvočíselná veta (dokázaná v 1896):

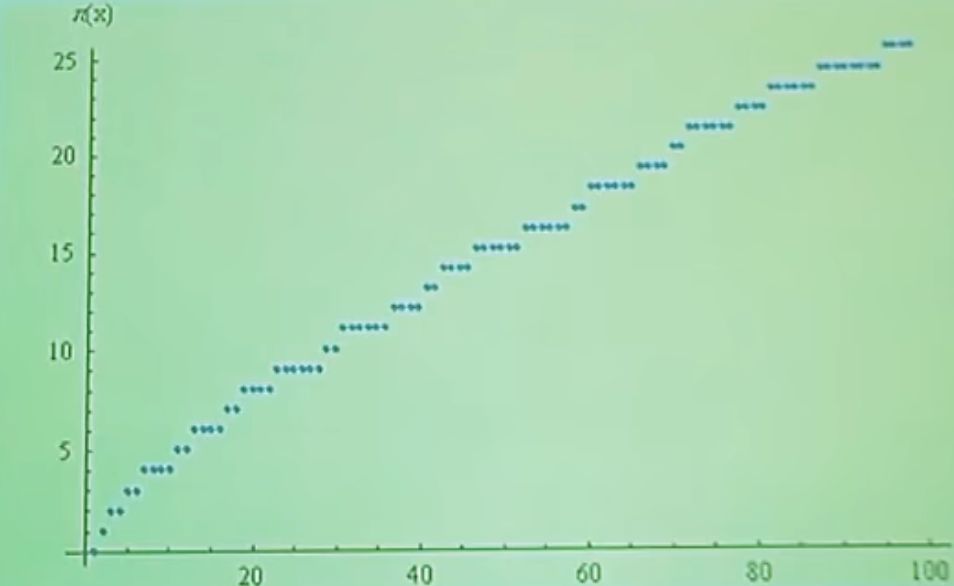
Obr. č.1 Funkcia π(x) v závislosti od x, zdroj: M. Rokyta

Prvočíselná veta hovorí o tom, že či existuje nejaká funkcia, ktorá by nám aproximovala funkciu π(x). Teda tak, že platí:

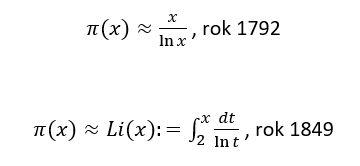
Tieto dve funkcie ohraničujú zhora a zdola našu π(x) , viď. obr.2.

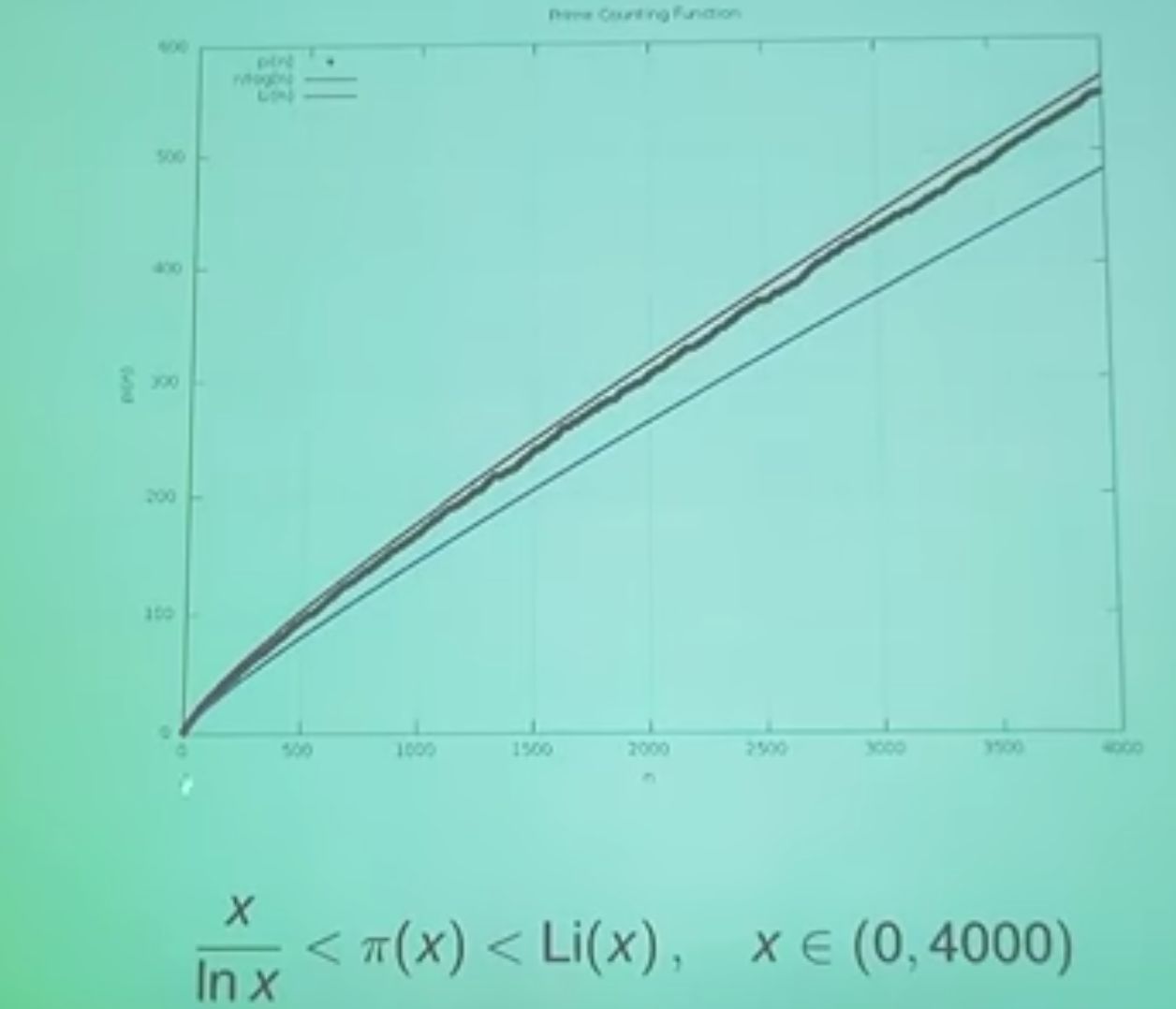
Obr. č.2 Uzavretie funkcie π(x), prvočíselná veta, zdroj: M. Rokyta.

Wolfram pi(x) výpočet, do zátvorky udať hodnotu:

https://www.wolframalpha.com/input/?i=pi%281001%29

Riemannova - zeta funkcia

Táto funkcia je definovaná predpisom: 

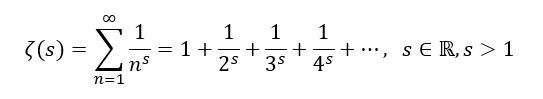
Pričom Zeta funkcia je analyticky predĺžená aj pre s<1, dokonca aj pre komplexné čísla C. Prepíšme teda túto funkciu pre analytické predĺženie: 

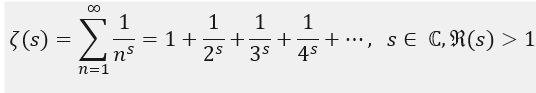
Riešením je: 

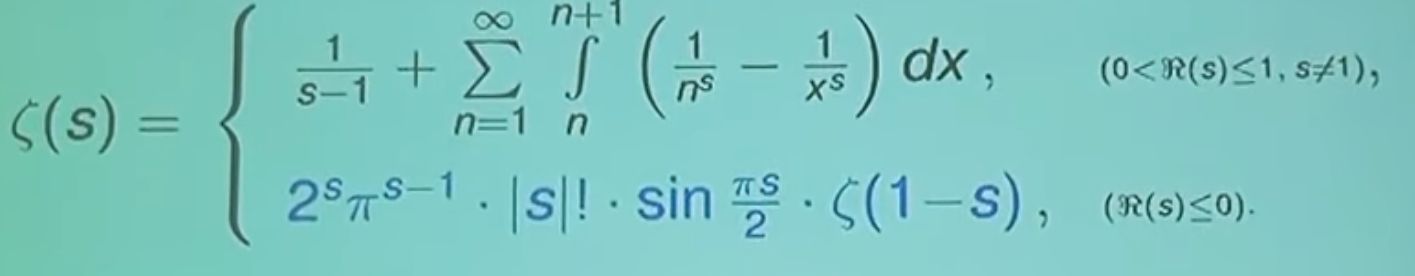
Základné korene vynesme do obr. č.3.

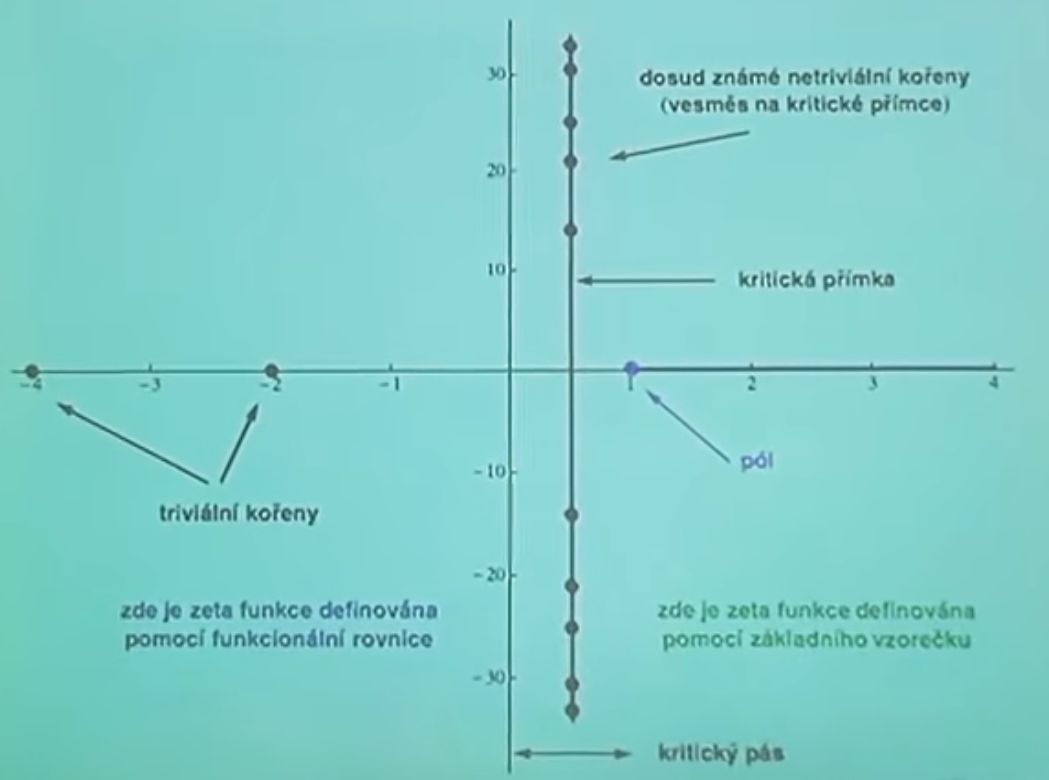
Obr.3 Korene Zeta funkcie, zdroj: M. Rokyta. 

Riemanova hypotéza teda hovorí, že všetky netriviálne korene analytického predĺženia funkcie do komplexnej roviny ležia na kritickej priamke prechádzajúcej cez 1/2.

Pekné video pre ilustráciu zeta funkcie je tu:

https://www.youtube.com/watch?v=sD0NjbwqlYw

ide naozaj o pôvabnú funkciu.

Prepojenie zeta funkcie na prvočísla

Euler (1737)

Euler našiel priame prepojenie zeta funkcie s prvočíslami, ktoré je platné a dokázané:

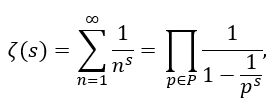
Ľavá strana: Pričom s >1, sčítame cez všetky prirodzené čísla.

Pravá strana: násobíme (symbol domčeka) cez všetky prvočísla.

Toto je priamy súvis so zeta funkciou. Práve preto je Riemannova hypotéza prepojená s prvočíslami.

Definujme Riemannovú funkciu:

Riemann (1859)

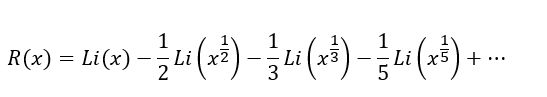
R(x) – je Riemannova funkcia

Li – funkcia Gaussova, viď vyššie, def. cez integrál

Vzťah súvisí s MÖbiovou funkciou

Ak Riemannova hypotéza platí potom:

Je Prvočíselná funkcia π(x) rovná presne:

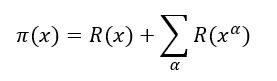
Pričom posledný člen sa sčíta cez všetky netriviálne korene alpha.

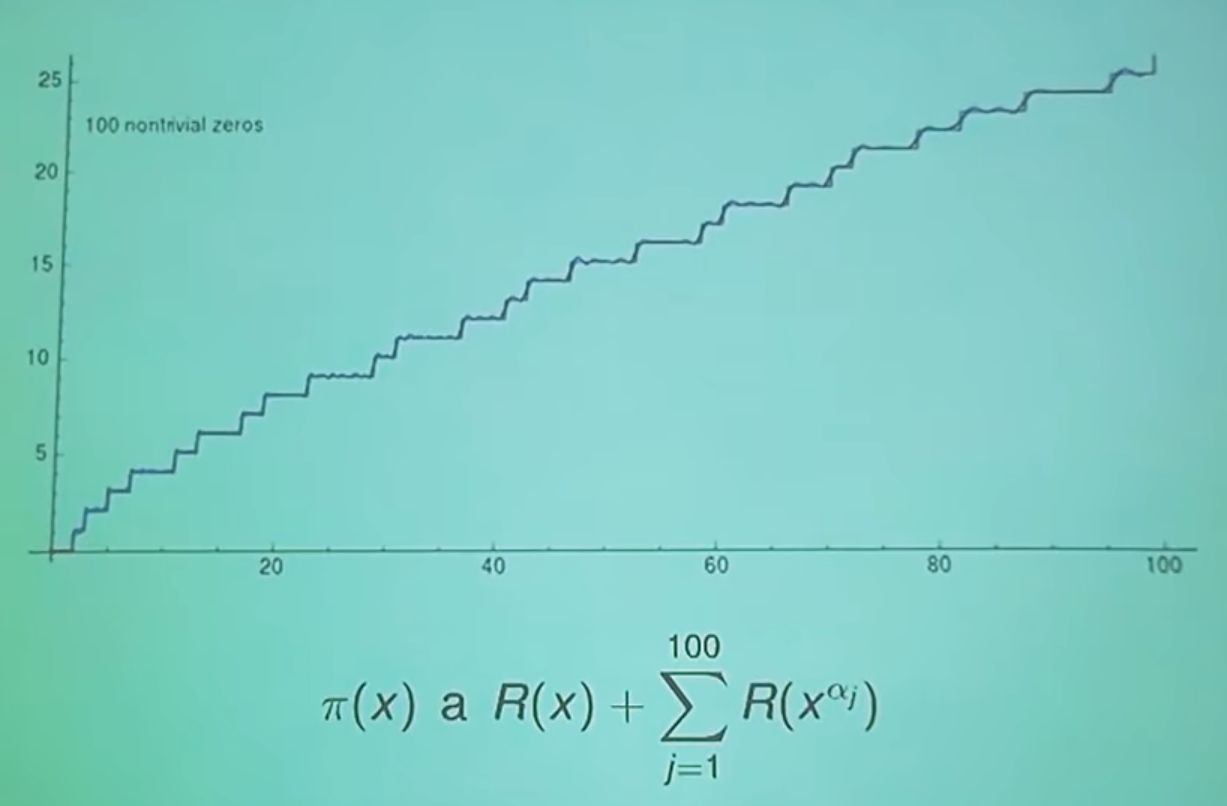
Obr. 4 Preložená Riemanová funkcia aproximuje presne π(x) v nekonečnom rade.

Pripomína to Fourierov rozklad. Teda pripočítavaním a odčítavaním prírastkov čoraz lepšie aproximujeme π(x).

Otázka znie, ako rýchlo konverguje táto funkcia? Pretože sa jedná o súčet nekonečného radu presný výsledok by sme dostali, až spočítaním nekonečných členov. Teda to vyzerá tak, že s istotou teda P=1 (100% pravdepodobnosť) sa nedá prehlásiť o žiadnom dostatočne veľkom čísle (to, čo nemôžeme z princípu preveriť faktorizáciou), či je alebo nie je prvočíslo.

Bakalárka na túto tému (v CZ jazyku):

https://is.muni.cz/th/ayifn/Bakalarka.pdf

Wolfram matematica:

Riemannova zeta funkcia, výpočet

https://www.wolframalpha.com/input/?i=riemann%20zeta%20function

Platnosť Riemannovej hypotézy

Základná, kľúčová otázka je tá, či platí, resp. neplatí Riemannova hypotéza?

Odpoveď: Zdá sa, že Riemannova hypotéza platí. Dôkaz však doposiaľ neexistuje. Matematici tvrdia, že sa jedná o najťažší miléniový problém. NA dôkazoch pohoreli aj tí najslávnejší matematici (Riemann, Hilbert, Turing, Selberg ...).

Doposiaľ sme numericky (na počítačoch) zistili, že:

• Nenašli sme žiadny koreň mimo kritickej priamky (kritického pásu).
  
• Preverili sme zhruba 10 exp 36 koreňov, to je číslo s 36 nulami za číslom.
  

Samozrejme aj také vysoké číslo je oproti nekonečnu zanedbateľné. Dôkaz Riemannovej hypotézy sa musí týkať celej číselnej osi. Prakticky však, ak preveríme ešte väčší počet koreňov kritickej priamky (nenájdeme koreň) mimo môžeme považovať rozmiestnenie prvočísiel v určitom intervale za potvrdené.

To, že sme nenašli koreň mimo ukazuje dobré vyhliadky pre platnosť Riemannovej hypotézy.

Vieme však, že všetky korene ležia blízko kritickej priamky.

ROBOPOL TESTOVANIE RIEMANNOVEJ HYPOTÉZY:

Séria článkov:

odkaz na články: (robopol výskum)

Publikácia: Evidence of equivalent conditions for the Riemann Hypothesis

Alternatívne cesty k dôkazu

1970 (Mongomery, Dyson) zistili, že:

Štatistické rozloženie známych koreňov na kritickej priamke je rovnaké ako štatistické rozloženie tzv. vlastných čísiel Hermitovských matíc. Tie matice popisujú rozloženie energetických hladín atómových jadier a úzko súvisí aj s inými  kvantovými javmi.

Michal Berry:

Pokiaľ by sme našli fyzikálny (kvantový), dynamický systém, ktorého vlastné čísla by presne zodpovedali koreňom Riemannovej funkcie, tak by tieto korene museli ležať na kritickej priamke. Pričom by sme takto dokázali Riemannovu hypotézu.

Poznámka:

Toto považujem za dobrý, alternatívny nápad k tomu, aby sme dokázali Riemannovu hypotézu. Obávam sa však, že aj pri existencii takéhoto kvantového systému sa nepodarí preukázať pre všetky korene. Dôvod je celom jednoduchý. Ak preukážeme zhodu takéhoto dynamického systému s koreňmi Riemannovej funkcie na určitom intervale, neznamená to automatický, že získame dôkaz pre celú kritickú priamku. Teda ja osobne si myslím, že takto sa to dokázať nedá, budeme riešiť aj pri existencii takéhoto kvantového systému, len trocha iný, taktiež ťažký problém.

Ďalší nápad bol, či neexistuje v rozostupe koreňov na kritickej priamke nejaký vzor s periódou?

Znova, pokiaľ by sme aj našli vzor s periódou neznamená to automaticky, že existuje len jeden vzor s jednou periódou. Práve naopak myslím si, že rozloženie prvočísiel nemá jednu periódu, jeden opakujúci sa vzor. To prečo si to myslím vychádza z vlastnosti prvočísiel popísaných v úvode v súvislosti s tvrdeniami A, B.

Poznámka: To, čo je ale troška zarážajúce je to, že sme skúmanie prvočísiel nahradili za skúmanie zeta funkcie. Miléniový problém nie sú prvočísla a ich rozloženie, ale zeta funkcia a jej kritická priamka. No zistil som, že veľa matematických konštrukcií už stavia na Riemannovej hypotéze, takže aj preto je zeta funkcia dôležitá!

RSA šifrovanie

=Pokračovanie v ďalšom diely=