Úvod
Tento diel je pokračovaním na predchádzajúci diel: Riemannova hypoteza-dodatok. (diel obsahuje aj kód v Pythone na preverenie rôznych vzťahov). Bez preštudovania predchádzajúcich dielov nebude tento článok zrozumiteľný pre čitateľa. V tomto článku budem hľadať analytický dôkaz ( modifikovaných, ekvivalentných tvrdení o RH, ako urobil v minulosti Srinivasa Ramanujan (Ramanudžan), Lagarias, Gronwall ,Robin ). V prípade, že čitateľa niečo zaujímavé napadne pri aktuálnom probléme, ktorý sa snažím vyriešiť budem rád za reakciu (emailom). Tento diel priamo nadväzuje na predchádzajúci diel, ktorý už obsahuje kapitolu - hľadanie analytického dôkazu.Referencie z ktorých vychádzam:
(1) RAMANUJAN, ROBIN, HIGHLY COMPOSITE NUMBERS, AND THE RIEMANN HYPOTHESIS
(2) http://math.colgate.edu/~integers/l33/l33.pdf
(3) Prime_number_theorem
(4) Numerical Evaluation of the Lambert W Function
POZNÁMKA: log x=ln x, vo vzťahoch nižšie je log x - prirodzený logaritmus.
V predchádzajúcom diely sú odvodené tieto dôležité vzťahy:

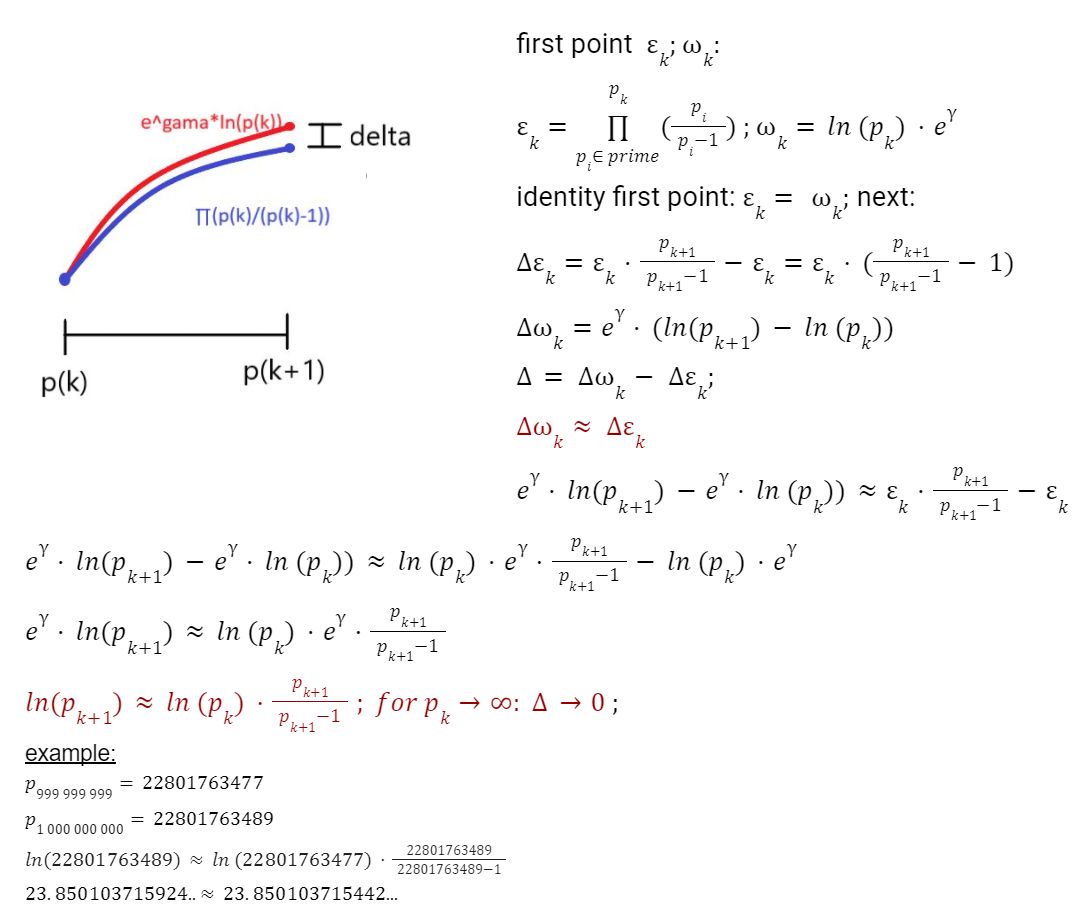
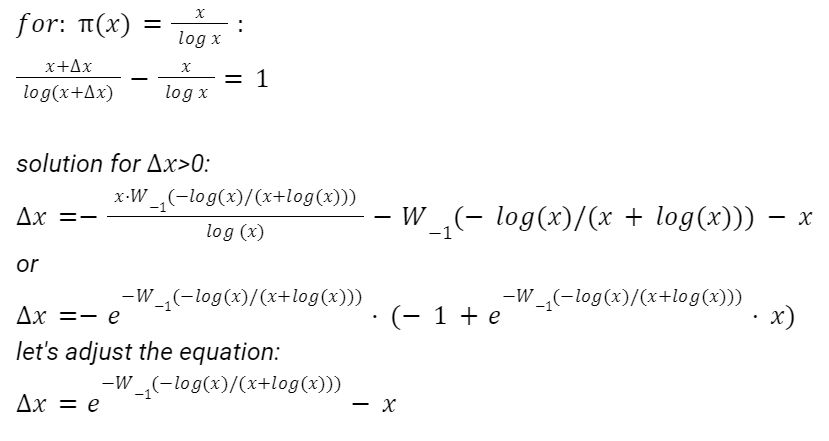
Obr.1 Niektoré dôležité odvodenia z predchádzajúceho dielu.
V minulom diely je rozpracovaný pokus o dôkaz pre hypotézu, že pokiaľ je sklon krivky (aproximácia x/(ln x -1-epsilon) väčší(rovný) na celom definičnom obore ako odvodený vzťah log(x+delta_x)>=log(x)*(x+delta_x)/(x+delta_x-1) (vid. predchádzajúci diel), potom by to znamenalo, že ekvivalentné podmienky pre RH musia platiť tiež.
Počiatočný bod p(k) je stotožnený pre ľubovolný bod x z aproximácie pi(x). Nárast hodnoty pi(x) o 1, znamená, že ďalšie prvočíslo je na hodnote x+delta_x. Z Robopol teorému plynie, že ak je splnený vzťah: log(x+delta_x)>=log(x)*(x+delta_x)/(x+delta_x-1) na celom definičnom obore, potom ekvivalentné podmienky pre RH platia tiež.
To je niečo podobné ako porovnávať derivácie v ľubovolnom bode x. Má to veľkú výhodu v tom, že nemusíme rátať predchádzajúce body (predchádzajúce prvočísla a podobne, násobiť ich medzi sebou). Hypotéza o menšom sklone (v ľubovolnom x) nemusí platiť, to neznamená neplatnosť ekvivalentných podmienok pre RH, no ak platí, že sklon je vždy menší, potom z toho plynie, že ekvivalentné podmienky pre RH musia platiť tiež.
1) Pozrime sa, či sa nedá nájsť analytické riešenie rovnice log(x+delta_x)>=log(x)*(x+delta_x)/(x+delta_x-1):

To znamená, že existuje analytické riešenie tejto rovnice. Uvidíme, či to pomôže pri porovnávaní s analytickým riešením rovnice pre aproximáciu pi(x).
2) Teraz je potrebné, aby sme upravili rovnicu pre pi(x), tak aby sme miesto premennej t mohli použiť x, potom dostaneme:
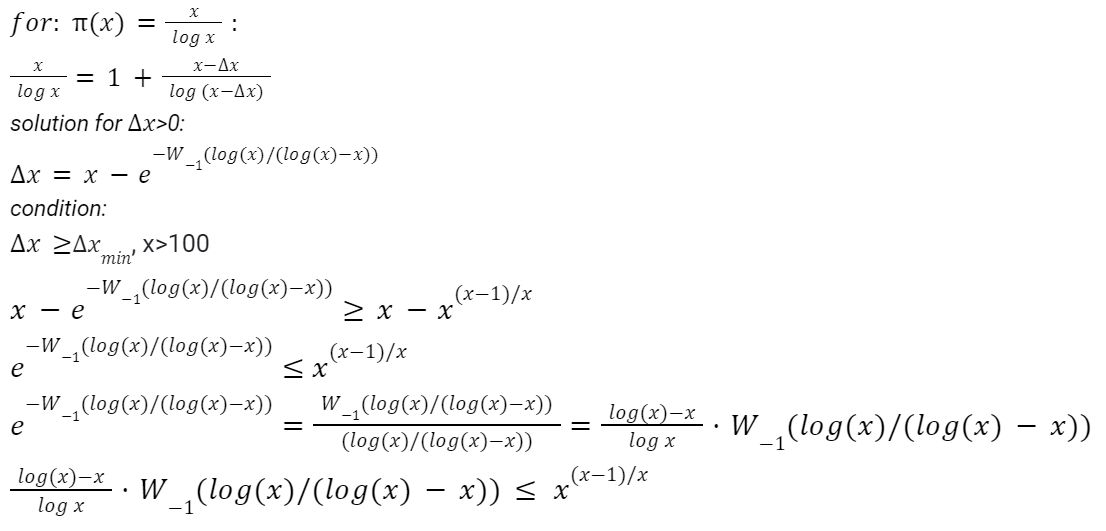
Z riešenia rovnice vidíme, že delta_x je veľmi podobné predchádzajúcej rovnici. Teraz potrebujeme preveriť výslednú nerovnosť a jej platnosť pre x >100.
Pre jednoduché dosadenie naozaj veľkých čísiel (napr. vo Wolframe) je podmienka splnená, poďme teda vytvoriť limitu, čomu sa tento vzťah rovná:

Obr. 2 Výpočet limity vzťahu pre pi(x)=x/log(x)
Result:
No a Wolfram nedokáže vypočítať túto limitu, nedokáže nám ani povedať či je číslo kladné, alebo záporné.
Poďme to preskúmať hlbšie. Najskôr preveríme pravú stranu vzťahu x^((x-1)/x) , urobíme deriváciu a limitu:
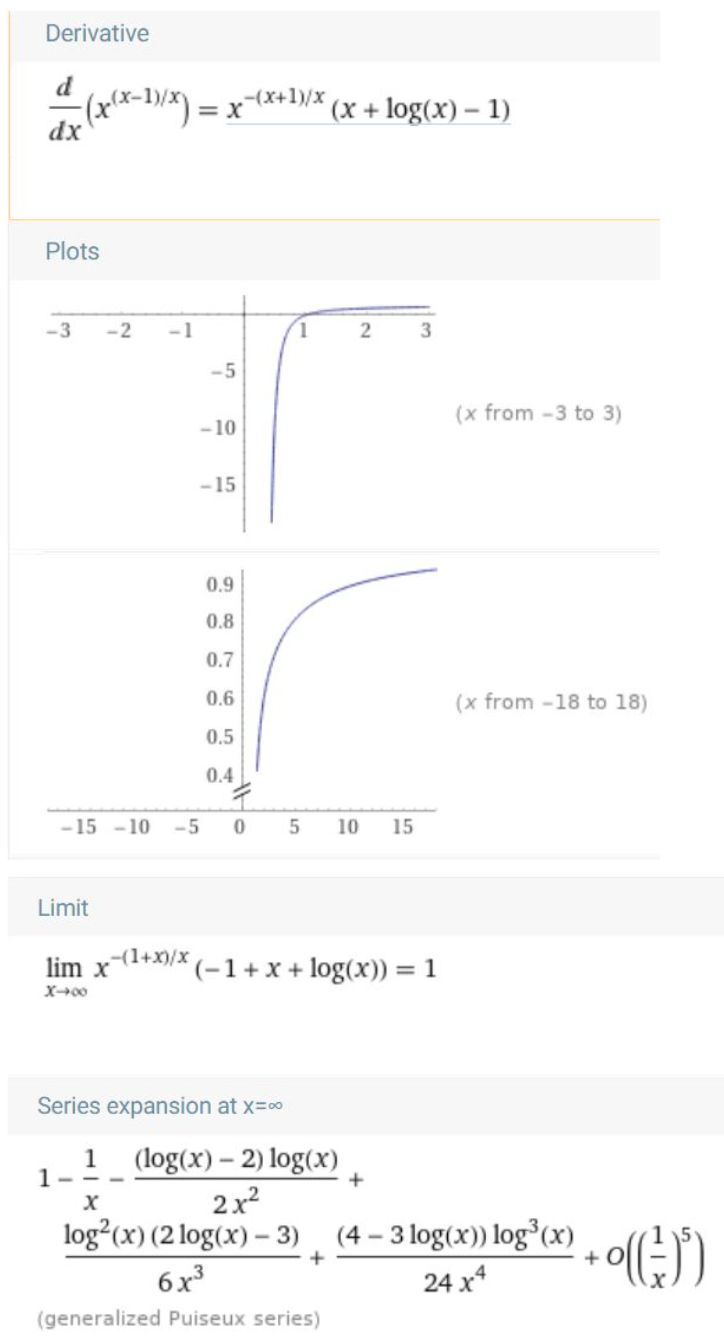
Obr.3 Derivácia a limita vzťahu x^((x-1)/x)
Teraz sa pozrime na tu W- funkciu:
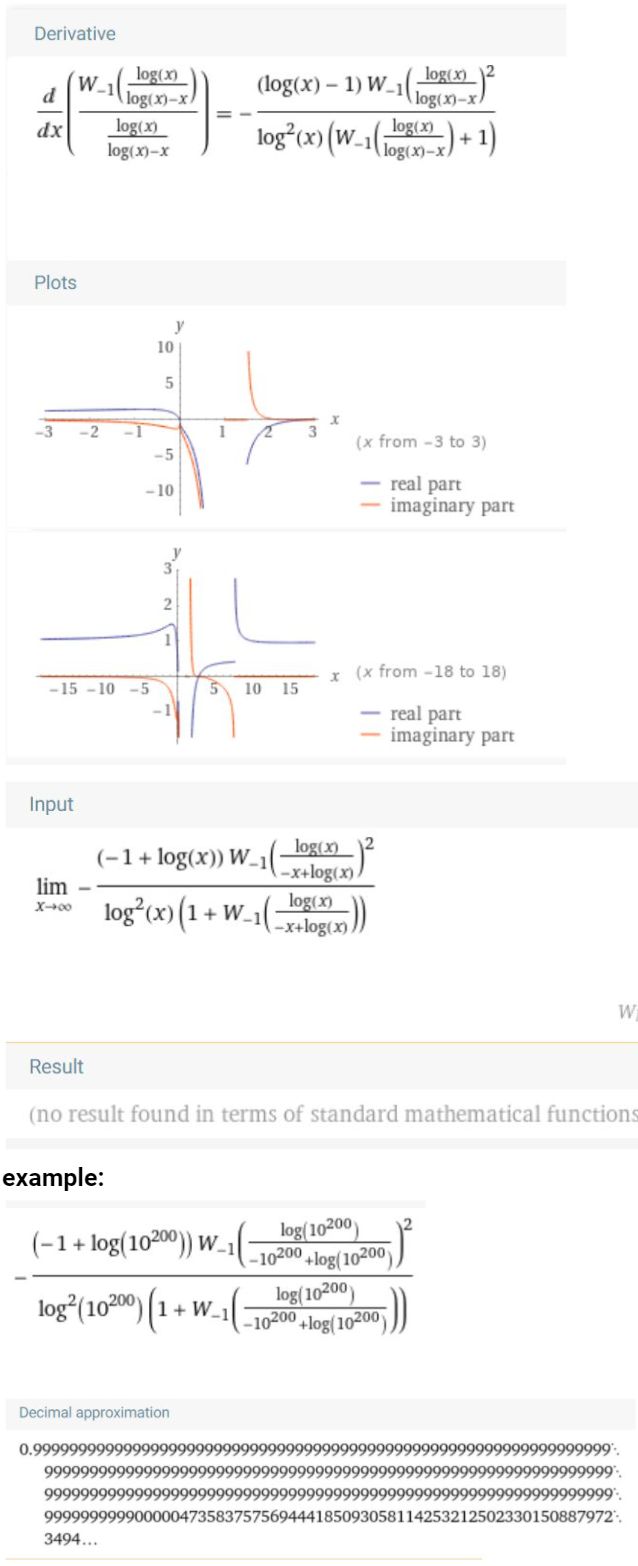
Obr. 3 derivácia, limita, príklad pre W-funkciu na ľavej strane
Vyhodnotenie:
Pokúsil som sa porovnať vzťahy pre limity, no ani ja ani Wolfram nenašiel korektné riešenie. Bohužiaľ inverznú Labertovú funkciu: W-1, teda productlog(-1,x), ktorá sa vo vzťahu na ľavej strane nerovnosti objavila nie je ani jednoduché rozviesť do Taylorového rozvoja. Pokúsil som sa porovnať derivácie týchto funkcii v zmysle obr. 3 a pre obe strany derivácie rýchlo konverguje k 1. Z príkladu vidieť, že derivácia W- funkcie je stále o niečo väčšia ako derivácia x^((x-1)/x).Príklad, kde si môžete pozrieť výsledky pre rôzne x - odkaz. Pri dosadzovaní (z numerického testu) sa hodnoty približovali k 1, z čoho plynie, že aj samotná limita bude zrejme 1. No úplne korektne to neviem doposiaľ dokázať. No záver je ten, že uvedená nerovnosť pre aproximáciu pi(x)=x/log x je zrejme splnená až do nekonečna, pretože derivácie týchto funkcii smerom k nekonečnu spejú k 1. Uvedené rovnice umožňujú preveriť nerovnosť ľubovolne ďaleko.
2) Výpočet pre aproximáciu pi(x)=x/(log x -1)
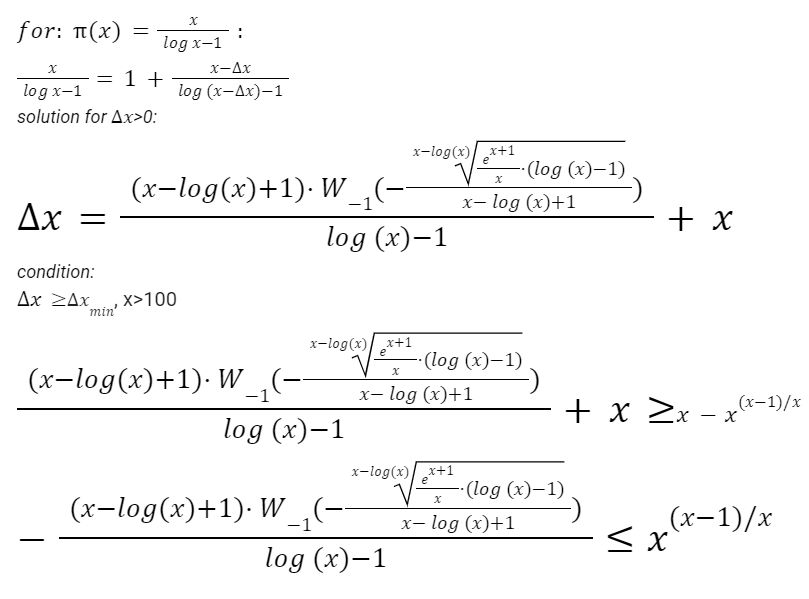
Pri dosadení veľkých čísiel zistíme, že podmienka je splnená:
Príklad:

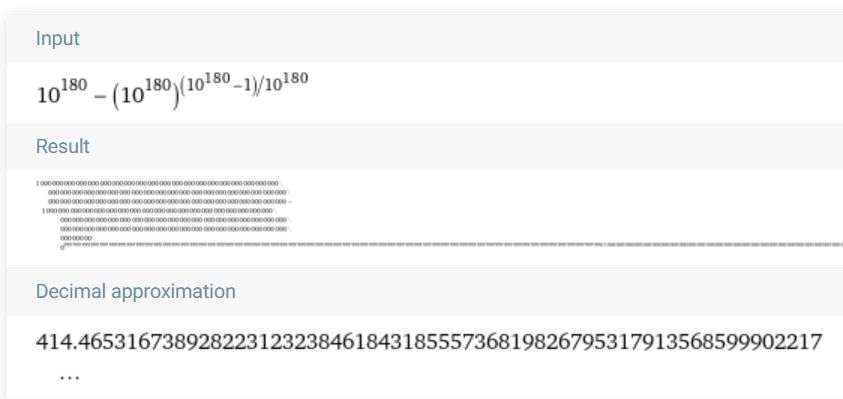
Obr.4 Test platnosti rovnice
Derivácia analytického riešenia pre delta_x:
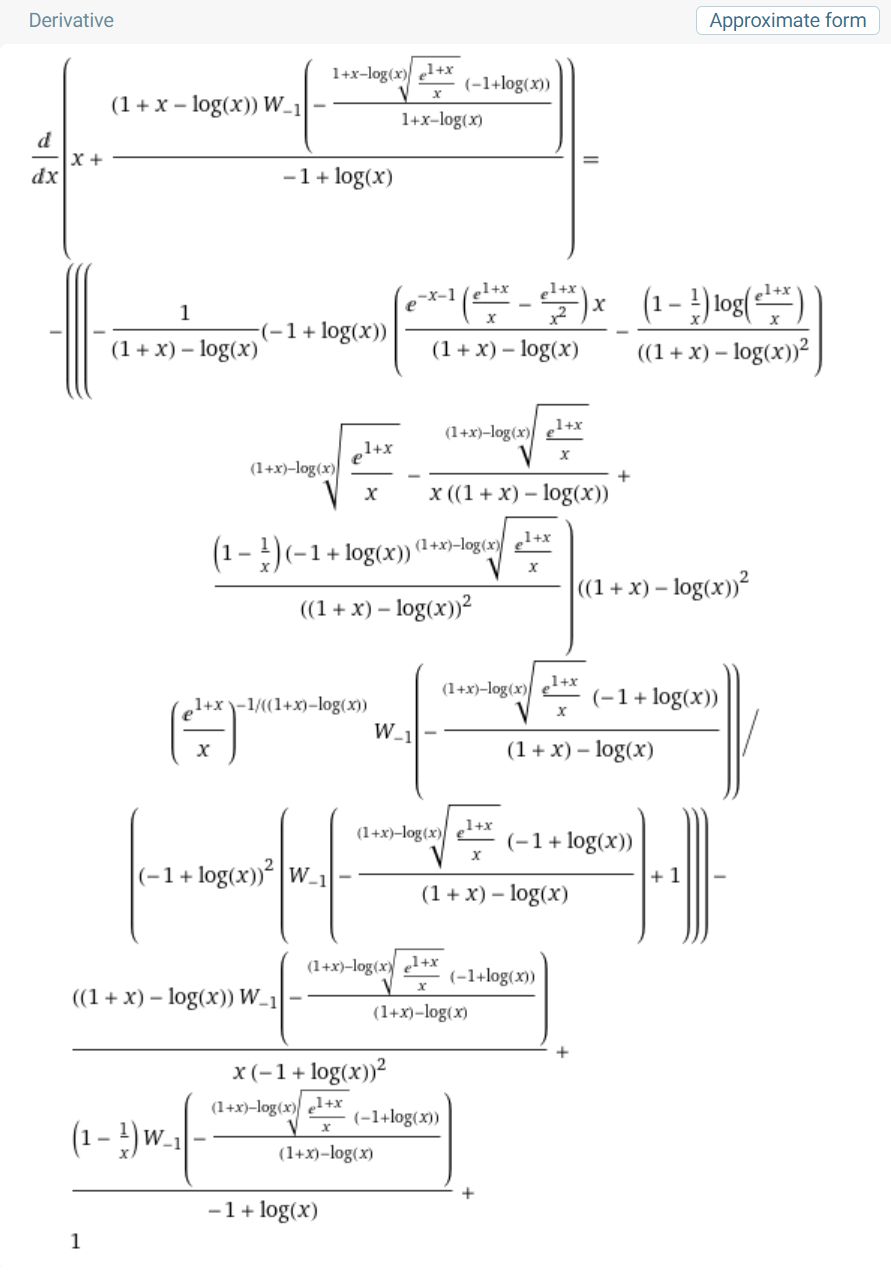
obr.5 Derivácia analytického riešenia pre delta_x
Vyhodnotenie:
Obdobne dopadla aj aproximácia pi(x)=x/(log x -1) v porovnaní s predchádzajúcou aproximáciou pi(x)=x/log x. Derivácia taktiež konverguje ku 1 pri manuálnom dosadení do vzťahu. Limita tejto komplikovanej funkcie sa taktiež nedá jednoducho zistiť, keďže obsahuje aj Lambertovú funkciu W-1. Zrejme teda platí aj pre túto aproximáciu, že uvedené vzťahy budú platiť až do nekonečna. Resp. je možné ich preveriť ľubovolne ďaleko.
3) Výpočet pre aproximáciu pi(x)=x/(log x -epsilon)
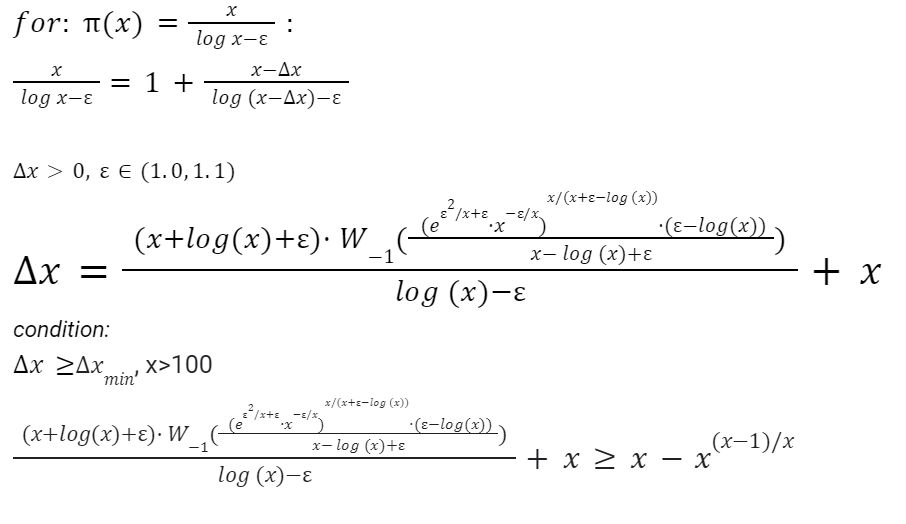
Obr.6 Odvodené analytické riešenie pre aproximáciu pi(x)=x/(log x -epsilon)
V zmysle referencie (3) - Prime number theorem je vzťah:
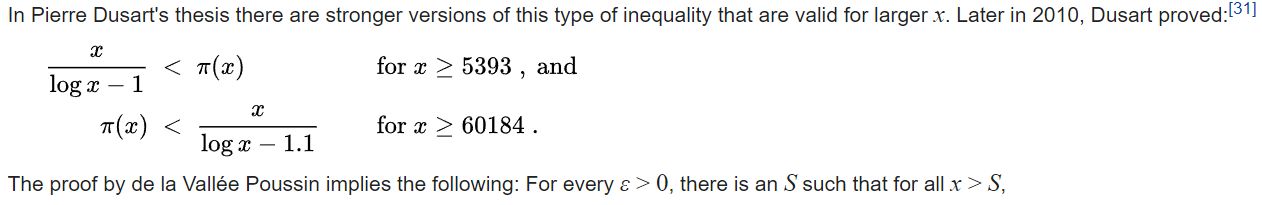
Teda pre akékoľvek nenulové epsilón je aproximácia väčšia ako pi(x). Pri testovaní epsilón sa dá zistiť nasledujúca závislosť:
Uvedený vzťah je vždy väčší ak platí epsilon=1+1/x. Teda napríklad pre x=10^15 musí byť hodnota epsilón=1+1/10 ^15 . V odkaze pre sústavu rovníc si môžete overiť túto závislosť - odkaz. Ak však bude epsilón väčší nerovnica nebude splnená (viď. vyššie). Teda aproximácia pi(x)= pi(x)=x/(log x -1) je v zmysle nerovnosti tá kritická hranica.
Záver
Z uvedených vzťahov sa dá tvrdiť, že pokiaľ je lim pi(x), x->infinity = lim x/(log x -1), x->infinity, potom uvedené vzťahy ukazujú, že ekvialetné podmienky pre RH by platili. No keďže sa nepodarilo vyrátať limitu korektne pre x=infinity nie je to možné považovať za exaktný dôkaz. No zároveň vzťahy umožňujú preveriť túto nerovnosť (viď. vzťahy obr.4) pre ľubovolné x. Tu v článku boli preverené vzťahy do hodnoty zhruba 10 ^ 500. Zároveň odvodené vzťahy môžu napomôcť aj na iné účely, ako je preverenie RH. Možno v budúcnosti, ak sa podarí vyriešiť limitu analyticky presne bude článok doplnený(resp. z dôvodu veľkosti bude vytvorený nový článok).Vzťah pre výpočet W-1 ukazuje referencia 4:

Podarilo sa obísť problém zložitosti Lambertovej W-1 funkcie a dosiahol sa overený výsledok výpočtu limít. Pokračovanie v článku - dôkaz-ekvivalentnych-podmienok-pre-riemannovu-hypotézu.